Question

A bank employs three tellers. A teller requires, on average, 10 minutes to process a customer’s transaction and customers arrive at the bank at the rate of 15 per hour. Service time follows an exponential distribution and arrival rate follows a Poisson distribution. What is the probability that an arriving customer will have to wait in line before being served? Round your answer to three decimals

Answer 1

To calculate the probability that an arriving customer will have to wait in line before being served, we use the formulas for an M/M/1 queue. Substituting the given values, the probability is approximately 0.042.

Step-by-step explanation:

To find the probability that an arriving customer will have to wait in line before being served, we need to calculate the average arrival rate and the average service rate. In this case, the arrival rate is given as 15 customers per hour, which translates to 15/60 = 0.25 customers per minute. The service rate can be calculated by taking the average service time of 10 minutes per customer and taking its reciprocal: 1/10 = 0.1 customer per minute.

Using the formulas for an M/M/1 queue, where the arrival rate follows a Poisson distribution and the service time follows an exponential distribution, we can calculate the probability of waiting in line using the following formula:

P(waiting in line) = (arrival rate/service rate)^(number of servers) / (number of servers * factorial(number of servers)) * (1 - (arrival rate/service rate))

Substituting the given values, we get:

P(waiting in line)
`= (0.25/0.1)^3 / (3 * factorial(3)) * (1 - (0.25/0.1))`

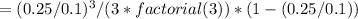
P(waiting in line) ≈ 0.042