Question

A rod starts from its left side and for 36 cm it is made of iron with a density of 8 g/cm3. The remaining 44 cm of the rod is made of aluminum with a density of 2.7 g/cm3

How far from the left end of the rod is its center of mass of in cm?

Answer 1

The center of mass for the given rod is ≈ 29.68 cm from the left end.

How to determine the center of mass for the given rod?

Given the rod with distinct sections:

1. Iron Section:

Length (L1) =
`36 cm`

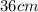
Density (ρ1) =
`8 g/cm^3`

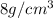
Mass (m1) =
`L1 * \rho1 = 36 cm * 8 g/cm^3 = 288 g`

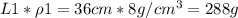
2. Aluminum Section:

Length (L2) =
`44 cm`

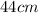
Density (ρ2) =
`2.7 g/cm^3`

Mass (m2) =
`L2 * \rho2 = 44 cm * 2.7 g/cm^3 = 118.8 g`

3. Total Mass (M):

`M = m1 + m2 = 288 g + 118.8 g = 406.8 g`

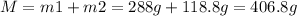
4. Center of Mass (x):

The center of mass is denoted by considering the weighted positions of each section:

x1: Distance from the left end to the center of mass of the iron section (x1 = L1/2 = 18 cm)

x2: Distance from the left end to the center of mass of the aluminum section (x2 = L1 + L2/2 = 80 cm)

Using the formula:

`x = (m1 * x1 + m2 * x2)/(M)`

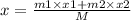
Substituting the values:

`x= \frac{288 \, \text{g} * 18 \, \text{cm} + 118.8 \, \text{g} * 80 \, \text{cm}}{406.8 \, \text{g}} \approx 29.68 \, \text{cm}`

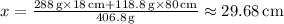
Hence, the center of mass for the given rod is approximately 29.68 cm from the left end.