Question

in a device known as an atwood machine, two masses m1 = 10 kg and m2 = 20kg are connected by rope over a frictionless pulley. what is the acceleration of each mass if the rope is massless?

Answer 1

In an Atwood machine with masses of 10 kg and 20 kg, the acceleration of each mass is 1/3 m/s^2.

Step-by-step explanation:

In an Atwood machine, two masses are connected by a rope over a frictionless pulley. In this case, the masses are m1 = 10 kg and m2 = 20 kg, and the rope is assumed to be massless. To find the acceleration of each mass, we can use the equation:

a = (m2 - m1) / (m1 + m2)

Substituting the values of m1 and m2 into the equation, we get:

a = (20 kg - 10 kg) / (10 kg + 20 kg) = 10 kg / 30 kg = 1/3 m/s2

Therefore, the acceleration of each mass in the Atwood machine is 1/3 m/s2.

Answer 2

For every mass, the acceleration is
`-4.91 m/s^2.`The acceleration is downward, as indicated by the negative sign.

To solve this problem

Two masses,
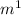`m^1` and
`m^2,` are connected by a rope across a frictionless pulley in an Atwood machine. The net force on each mass is the difference between the mass's weight and the tension in the rope, which is the same on both sides of the rope.

The net force on mass
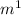`m^1`is:

`F1 = m^1g - T`

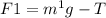
The net force on mass
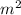`m^2`is:

`F2 = T - m^2g`

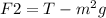
Since the system is in motion, the net force on each mass must be equal to the mass times its acceleration. so, we can set the two equations equal to each other:

`m^1g - T = m^2a`

`T - m^2g = m^1a`

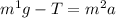
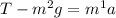
Solving for T in the second equation, we get:

`T = m^1a + m^2g`

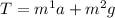
Substituting this expression for T into the first equation, we get:

`m^1g - (m^1a + m^2g) = m^2a`

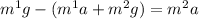
Now, let combining like terms, we get:

`(m^1 - m^2)g = (m^1 + m^2)a`

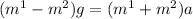
Solving for a, we get:

`a = (m^1 - m^2)g / (m^1 + m^2)`

Plugging in the values of m1 and m2, we get:

`a = (10 kg - 20 kg) * 9.81 m/s^2 / (10 kg + 20 kg)`

`a = -4.91 m/s^2`

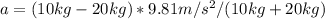
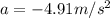
So, For every mass, the acceleration is
`-4.91 m/s^2.` The acceleration is downward, as indicated by the negative sign.