Question

select all of the following that are potential roots of p(x) = x4 − 9x2 − 4x 12? 0 ±2 ±4 ±9 ±3 ±6 ±12

Answer 1

The potential roots of the polynomial
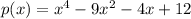`p(x) = x^4 - 9x^2 - 4x + 12` are divisors of the constant term, hence potential rational roots include ±2, ±3, ±4, ±6, and ±12.

Step-by-step explanation:

To find the potential roots of the polynomial
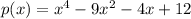`p(x) = x^4 - 9x^2 - 4x + 12`, we can use the Rational Root Theorem. However, there seems to be a typo in the given polynomial, as the coefficients should align properly. Assuming the polynomial is correctly written, the Rational Root Theorem suggests that the potential rational roots are the divisors of the constant term (in this case, ±1, ±2, ±3, ±4, ±6, ±12) divided by the divisors of the leading coefficient (which is 1 in this case).

The potential roots given in the question are 0, ±2, ±4, ±9, ±3, ±6, ±12. Since the leading coefficient is 1, we can directly consider the divisors of the constant term, 12. Among the options provided, ±2, ±3, ±4, ±6, and ±12 could be potential roots based on the Rational Root Theorem. To determine which, if any, of these potential roots are actual roots, we would substitute them into the polynomial and see if the result is zero.

Answer 2

±2, ±3 are potential roots of the polynomial p(x) =
`x^4 − 9x^2 − 4x − 12.`

Step-by-step explanation:

To find potential roots of the polynomial, we can use the Rational Root Theorem. According to this theorem, potential roots are the divisors of the constant term (in this case, 12) divided by the divisors of the leading coefficient (in this case, 1). The divisors of 12 are ±1, ±2, ±3, ±4, ±6, ±12, and the divisors of 1 are ±1. Therefore, the potential rational roots are ±1, ±2, ±3, ±4, ±6, ±12.

Now, we substitute each potential root into the polynomial and check for which values p(x) equals zero. After evaluating, we find that p(2) = 0, p(-2) = 0, p(3) = 0, and p(-3) = 0.

Therefore, ±2, ±3 are the roots of the polynomial. The other potential roots (±1, ±4, ±6, ±12) do not satisfy the equation. This is the reason they are not included in the final answer. Thus, the roots of the given polynomial are ±2, ±3.