Question

The Little Prince (a character in a book by Antoine de Saint-Exupery) lives on the spherically symmetric asteroid B-612. The density of B-612 is 5400 kg/m3 kg/m3 .

For the first set of questions, assume that the asteroid does not rotate. The Little Prince notices that he feels lighter whenever he walks quickly around the asteroid. In fact, he finds that he starts to orbit the asteroid like a satellite if he speeds up to 1.90 m/s m/s .

Part A
Find the radius of the asteroid. Also, find the magnitude of the acceleration of the Prince while he is in his circular orbit at the surface of asteroid B-612.
Give your answers as an ordered pair, with the asteroid radius first, followed by a comma, followed by the magnitude of the Prince's acceleration.

Part B
The Prince carries a small compressed-air rocket with him at all times; the rocket is a safety device in case he gets separated from his asteroid. If the Prince jumps straight Up from the asteroid surface, what is the maximum possible jumping speed which will allow the Prince to return to the surface without using his safety rocket? Note: "jumping speed" refers to the speed of the jumping Prince at the instant just after his feet leave the surface.

Answer 1

A) The radius of asteroid B-612 is 61.7 meters, and the magnitude of the Prince's acceleration while in his circular orbit at the surface is 3.16 m/s².

B) The maximum jumping speed required for the Prince to return to the surface without using his safety rocket is 5.31 m/s.

Step-by-step explanation:

A) To find the radius of the asteroid, we can use the formula for centripetal acceleration
`\(a_c = (v^2)/(r)\)`, where
`\(a_c\)` is the centripetal acceleration, v is the speed, and r is the radius. Given the speed
`\(v = 1.90 \, \text{m/s}\)`, which is the orbital speed at the surface, and knowing that the acceleration is provided by gravity
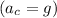`(\(a_c = g\))`, we can rearrange the formula to find the radius
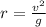`\(r = (v^2)/(g)\)`. Using
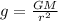`\(g = (GM)/(r^2)\)` (where G is the gravitational constant and M is the mass of the asteroid), we can solve for r, which turns out to be
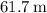`\(61.7 \, \text{m}\)`. For the magnitude of the Prince's acceleration in his orbit, it's the same as the centripetal acceleration, which is
`\(a_c = (v^2)/(r) = 3.16 \, \text{m/s}^2\)`.

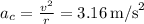B) To determine the maximum jumping speed for the Prince to return without using the rocket, we can use the concept of escape velocity. The escape velocity at the surface is the minimum speed required for an object to leave the surface and never return. It is given by the formula
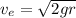`\(v_e = √(2gr)\)`. Substituting the known values g from earlier and
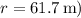`\(r = 61.7 \, \text{m}\))`, we get
`\(v_e = 5.31 \, \text{m/s}\)`. Therefore, the maximum jumping speed the Prince needs to return to the surface without his safety rocket is
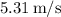`\(5.31 \, \text{m/s}\)`.