Question

Solve when the following function is below zero using the Algebraic method

g(x) = -1/6(x+3)^3(x-(3/2))(x-2)^2

Answer 1

`(-\infty, -3) \cup \left((3)/(2), 2\right) \cup (2, \infty)`

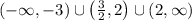
Explanation:

Given function:

`g(x) = -(1)/(6)(x+3)^3\left(x-(3)/(2)\right)(x-2)^2`

To solve the inequality g(x) < 0 for the given continuous function g(x), begin by finding the roots of the polynomial by setting each factor equal to zero and solving for x:

`x + 3 = 0 \implies x = -3`

`x - (3)/(2)= 0 \implies x = (3)/(2)`

`x - 2 = 0 \implies x = 2`

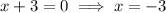
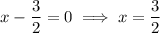
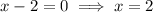
We need to consider the intervals between and beyond the found roots.

In this case, we have four intervals: (-∞, -3), (-3, 3/2), (3/2, 2), and (2, ∞).

Choose a value within each interval and substitute it into the function g(x), then determine whether the resulting value is positive or negative.

For the interval (-∞, -3), use x = 4:

`g(-4) = -(1)/(6)((-4)+3)^3\left((-4)-(3)/(2)\right)((-4)-2)^2 = -33 < 0`

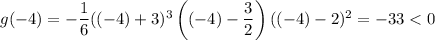
For the interval (-3, 3/2), use x = 0:

`g(0) = -(1)/(6)(0+3)^3\left(0-(3)/(2)\right)(0-2)^2 = 27 > 0`

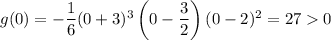
For the interval (3/2, 2), use x = 7/4:

`g(1.75) = -(1)/(6)\left((7)/(4)+3\right)^3\left((7)/(4)-(3)/(2)\right)\left((7)/(4)-2\right)^2 =-0.279... < 0`

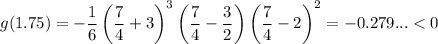
For the interval (2, ∞), use x = 3:

`g(3) = -(1)/(6)(3+3)^3\left(3-(3)/(2)\right)(3-2)^2 = -54 < 0`

From the above calculations, we can conclude that g(x) is below zero (negative) in the intervals (-∞, -3), (3/2, 2) and (2, ∞).

Therefore, the solution to the inequality g(x) < 0 is:

• (-∞, -3) ∪ (3/2, 2) ∪ (2, ∞)

(This solution assumes that there are no additional factors or constraints on the domain of the function g(x)).