Question

Three 104.0−g Ice cubes initially at 0⁰C are added to 0.890 kg of water initially at 24.0⁰C in an insulated container.

(a) What is the equilibrium temperature of the system?__⁰C
(b) What is the mass of unmelted ice, if any, when the system is at equilibrium?__ kg

Answer 1

(a) The equilibrium temperature of the system is 0.0°C.

(b) There is no mass of unmelted ice when the system is at equilibrium.

Step-by-step explanation:

When three ice cubes at 0°C are added to water at 24.0°C, heat transfer occurs until thermal equilibrium is reached. The heat gained by the ice as it melts equals the heat lost by the water as it cools down. Using the principle of conservation of energy, the final temperature is calculated using the formula:

`\(m_1c_1ΔT_1 + m_2c_2ΔT_2 = 0\)`

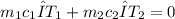
Where
`\(m_1\)` and
`\(m_2\)` are the masses of ice and water respectively,
`\(c_1\)` and
`(c_2\)` are their specific heats, and ΔT is the change in temperature.

The heat released by the water is equal to the heat absorbed by the ice to melt and warm up to the final equilibrium temperature. At equilibrium, all the ice melts, leaving no unmelted ice. Therefore, the final answer for the equilibrium temperature is 0.0°C, and there's no remaining mass of unmelted ice.

This calculation assumes no heat exchange with the surroundings and neglects any temperature change in the container itself. The equilibrium temperature represents the point at which both the ice and water have exchanged heat to reach a common final temperature, resulting in complete melting of the ice and no remaining unmelted ice in the system.

Answer 2

The solution to this physics problem involves calculating the heat exchange between ice cubes and warmer water in an insulated container to find the equilibrium temperature and any remaining ice mass.

Step-by-step explanation:

The student's problem involves finding the equilibrium temperature of a system and the mass of unmelted ice, if any, when three ice cubes at 0°C are added to warmer water at 24.0°C in an insulated container. To solve this, we consider the energy exchange between the ice cubes and the water without any heat loss to the surroundings because it is an insulated container. The heat gained by the melting ice comes from the heat lost by the warmer water. The temperature reached at equilibrium is determined by setting the heat lost by the water equal to the heat gained by the ice until it melts and assuming no further heat is required to raise the temperature of the resulting meltwater.

Firstly, we need to calculate the amount of heat required to melt the ice and see if there is enough heat in the water to completely melt the ice. If there's insufficient heat to melt all the ice, some will remain and the final temperature will be 0°C. If all the ice melts, the final temperature will be higher than 0°C and can be calculated using energy balance equations.