The magnitude of the velocity of the new asteroid after the collision is

To find the magnitude of the velocity of the new asteroid after the collision, you can use the principle of conservation of momentum, which states that the total momentum before the collision is equal to the total momentum after the collision.
The total momentum before the collision is the sum of the momenta of the two asteroids:
![\[ \text{Total momentum before collision} = m_A * v_A + m_B * v_B \]](https://img.qammunity.org/2024/formulas/physics/high-school/8o91d4lw9tv50oyjwnn7vivx8pwj7ss2gi.png)
Where:
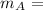 mass of asteroid
mass of asteroid
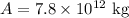
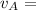 velocity of asteroid
velocity of asteroid

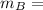 mass of asteroid
mass of asteroid
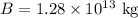
 velocity of asteroid
velocity of asteroid
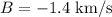 (negative because it's in the opposite direction)
(negative because it's in the opposite direction)
First, convert the velocities to a common unit, like meters per second:
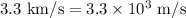
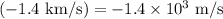
Now, calculate the total momentum before the collision:
![\[ \text{Total momentum before collision} = (7.8 * 10^(12) \text{ kg} * 3.3 * 10^3 \text{ m/s}) + (1.28 * 10^(13) \text{ kg} * (-1.4 * 10^3 \text{ m/s})) \]](https://img.qammunity.org/2024/formulas/physics/high-school/mnhgxx92sey3b3liw36x6jio8gq70of7qa.png)
Calculate this total momentum.
![\[ \text{Total momentum before collision} = (25.74 * 10^(15) \text{ kg m/s}) - (17.92 * 10^(15) \text{ kg m/s}) \]](https://img.qammunity.org/2024/formulas/physics/high-school/hgmtvt4co6z6blcqtmj4gb1q42lv9dxmc9.png)
![\[ \text{Total momentum before collision} = 7.82 * 10^(15) \text{ kg m/s} \]](https://img.qammunity.org/2024/formulas/physics/high-school/ea94h1g9x6rylkjlwkglxtmplygp8gnn12.png)
This total momentum must be conserved after the collision when the asteroids stick together.
Now, the total mass after the collision is the sum of the masses of the two asteroids:

![\[m_{\text{total}} = 2.06 * 10^(13) \text{ kg}\]](https://img.qammunity.org/2024/formulas/physics/high-school/bw5ix33477lmm0zbefb5z7450pbywhgw3b.png)
The velocity of the new asteroid after the collision can be found by using the conservation of momentum formula:
![\[ \text{Total momentum after collision} = m_{\text{total}} * v_{\text{new}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/ujxh994f7q2m5ojhxwcx8icg2mswgwhxa9.png)
Solve for
 :
:
![\[ v_{\text{new}} = \frac{\text{Total momentum before collision}}{m_{\text{total}}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/kuk3fbwzrkp6y15xjcyz4ej7xyc7e3htfg.png)
![\[ v_{\text{new}} = \frac{7.82 * 10^(15) \text{ kg m/s}}{2.06 * 10^(13) \text{ kg}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/8w73il8pwanlnaste2pi40059n3otkzdfn.png)
Solve for
 :
:
![\[ v_{\text{new}} = \frac{7.82 * 10^(15) \text{ kg m/s}}{2.06 * 10^(13) \text{ kg}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/8w73il8pwanlnaste2pi40059n3otkzdfn.png)
Now, perform the division to find the value of
 :
:
![\[ v_{\text{new}} = (7.82 * 10^(15))/(2.06 * 10^(13)) \text{ m/s} \]](https://img.qammunity.org/2024/formulas/physics/high-school/ldh18xe0axmrhedr16gg5vulwj7l98v0ym.png)
Simplify the expression:
![\[ v_{\text{new}} = 3.80 * 10^2 \text{ m/s} \]](https://img.qammunity.org/2024/formulas/physics/high-school/qdxmd6w5wb6iltd4ozho6azlh96un1ipoj.png)
The expression
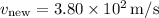 can be simplified further:
can be simplified further:
![\[v_{\text{new}} = 380 \, \text{m/s}\]](https://img.qammunity.org/2024/formulas/physics/high-school/dmpccz35atdazaggyk6pesi39yd1fsn4oh.png)
Therefore, The answer is
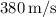 .
.
The complete question is here:
Two asteroids strike head-on: before the collision, asteroid A(mA=7.8×1012 kg) has velocity 3.3 km/s and asteroid B(mB=1.28×1013 kg) has velocity 1.4 km/s in the opposite direction.
If the asteroids stick together, what is the magnitude of the velocity of the new asteroid after the collision?
If the asteroids stick together, what is the direction of the velocity of the new asteroid after the collision? A.) in the original direction of asteroid B
OR B.) in the original direction of asteroid A