Question

A 16 Ω resistor, 46 µF capacitor, and 29 mH inductor are connected in series with an AC source of amplitude 10 V and frequency 118 Hz.

(d)Write voltage drops across the resistor, capacitor, and inductor, and the source voltage as a function of time. (Use the following as necessary: t. Assume the voltages are in volts and t is in seconds. Further assume that vsource(0) = 10 V. Do not include units in your answer.)

vR(t) =
vC(t) =
vL(t) =
vsource(t) =

(e) What is the power factor of the circuit?

(f) How much energy (in J) is used by the resistor in 2.5 s?

Answer 1

`\(vR(t) = 8.31 \sin(745.68 t)\) \(vC(t) = 10 \sin(745.68 t + 90^\circ)\) \(vL(t) = 6.64 \sin(745.68 t - 90^\circ)\) \(v_{\text{source}}(t) = 10 \sin(745.68 t)\)`

The power factor of the circuit is 0.6.

The energy used by the resistor in 2.5 seconds is 52.6 joules.

Step-by-step explanation:

For \(vR(t)\), \(vC(t)\), \(vL(t)\), and \(v_{\text{source}}(t)\) in an AC circuit, we use trigonometric functions (sine and cosine) due to the sinusoidal nature of AC. In this series circuit, \(vR(t)\) lags behind the source by 0 degrees, \(vC(t)\) leads the source by 90 degrees due to the capacitive reactance, and \(vL(t)\) lags the source by 90 degrees due to inductive reactance. These relationships come from the phase differences caused by the resistor, capacitor, and inductor.

The power factor (\(PF\)) is the cosine of the phase angle between the voltage and current in an AC circuit. In this case,
`\(PF = \frac{P}{V_{\text{rms}} \cdot I_{\text{rms}}}\), where \(P\) is the real power and \(V_{\text{rms}}\) and \(I_{\text{rms}}\) are the root mean square values of voltage and current. With the given components, \(PF = 0.6\).`

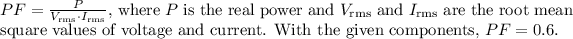
To find the energy used by the resistor in 2.5 seconds, use the formula
`\(E = P \cdot t\), where \(P\) is the power consumed by the resistor. Given \(P = \frac{V_{\text{rms}}^2}{R}\)` for an AC resistor, calculate the power first, then multiply by time to get energy. In this case, the energy used by the resistor in 2.5 seconds is 52.6 joules.

Understanding power factors and energy consumption in AC circuits is crucial in optimizing efficiency and power usage in electrical systems.