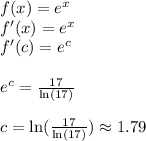Question

a. Determine whether the Mean Value Theorem applies to the function f(x)= ex on the given interval [0, In 17]. b. If so, find the point(s) that are guaranteed to exist by the Mean Value Theorem. a. Choose the correct answer below. O A. The Mean Value Theorem applies because the function is continuous on (0, In 17) and differentiable on [O, In 17). O B. The Mean Value Theorem does not apply because the function is not differentiable on (0, In 17). O C. The Mean Value Theorem does not apply because the function is not continuous on [0, In 17]. D. The Mean Value Theorem applies because the function is continuous on [0, In 17] and differentiable on (0, In 17). b. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. The point(s) is/are x = . (Type an exact answer. Use a comma to separate answers as needed.) O B. The Mean Value Theorem does not apply in this case.

Answer 1

MVT applies since function is continuous and differentiable over the interval

Point is x=1.79

Explanation:

The Mean Value Theorem (MVT) states that if a function f(x) is continuous on the interval [a,b] and differentiable on (a,b), then there is a value "c" such that
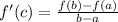`f'(c)=(f(b)-f(a))/(b-a)`, which is the average rate of change over [a,b].

Given
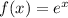`f(x)=e^x` is continuous on
`[0,\ln(17)]` and is differentiable on
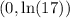`(0,\ln(17))`, MVT does apply and we can proceed with our calculations:

`f'(c)=(f(b)-f(a))/(b-a)=(f(\ln(17))-f(0))/(\ln(17)-0)=(17)/(\ln(17))`

`f(x)=e^x\\f'(x)=e^x\\f'(c)=e^c\\\\e^c=(17)/(\ln(17))\\\\c=\ln((17)/(\ln(17)))\approx1.79`