Question

A block of mass 2.30 kg is pushed 2.03 m along a frictionless horizontal table by a constant 20.0N force directed 23.0° below the horizontal. Determine the work done by the applied force (in Joules).

(8b) Determine the magnitude of the normal force exerted by the table.
(8c) Determine the magnitude of the force of gravity.
(8d) Determine the magnitude of the net force on the block.

Answer 1

The work done by the force is calculated by multiplying the horizontal component of the applied force with the distance moved by the block along the horizontal table.

Step-by-step explanation:

To determine the work done by the applied force on a 2.30 kg block, we need to consider only the component of the force that acts in the direction of the displacement. Since the force is applied at an angle of 23.0° below the horizontal, the horizontal component of the force is Fx = F × cos(θ) = 20.0 N × cos(23.0°). We can then calculate the work done by this force over a distance of 2.03 m as Work = Fx × distance.

Answer 2

1. The work done by the applied force is approximately 40.77 Joules.

2. The magnitude of the normal force exerted by the table is approximately 22.563 N.

3. The magnitude of the net force on the block is approximately 20.01 N.

Let's break down the problem into several parts:

(8a) Determine the work done by the applied force:

The work done by a force can be calculated using the formula:

Work (W) = Force (F) × Distance (d) × cos(θ)

Where:

• W is the work done (in joules).
• F is the force applied (in newtons).
• d is the distance over which the force is applied (in meters).
• θ is the angle between the force and the direction of motion.

In this case, F = 20.0 N, d = 2.03 m, and θ = 23.0°.

First, convert the angle from degrees to radians:

θ = 23.0° × (π/180) ≈ 0.40143 radians

Now, calculate the work done:

W = 20.0 N × 2.03 m × cos(0.40143 radians)

W ≈ 40.77 Joules

So, the answer is approximately 40.77 Joules.

(8b) Determine the magnitude of the normal force exerted by the table:

The normal force (N) is the force exerted by a surface to support the weight of an object resting on it when there is no vertical acceleration. In this case, it balances the gravitational force acting on the block.

The magnitude of the normal force is equal to the weight of the block:

Weight (W) = mass (m) × gravity (g)

Where:

• m is the mass of the block (2.30 kg).
• g is the acceleration due to gravity (approximately 9.81 m/s²).

W = 2.30 kg × 9.81 m/s² ≈ 22.563 N

So, the answer is approximately 22.563 N.

(8c) Determine the magnitude of the force of gravity:

We've already calculated the magnitude of the force of gravity in part 8b. It is approximately 22.563 N.

(8d) Determine the magnitude of the net force on the block:

The net force on the block can be calculated using Newton's second law:

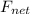`F_{net` = m × a

Where:

• 
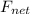  `F_{net` is the net force (in newtons).
• m is the mass of the block (2.30 kg).
• a is the acceleration (in meters per second squared).

Since the block is moving horizontally and there is no friction, the only horizontal force acting on it is the applied force of 20.0 N. Therefore, the acceleration is given by:

a = (20.0 N) / (2.30 kg) ≈ 8.70 m/s²

Now, calculate the net force:

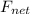`F_{net` = 2.30 kg × 8.70 m/s² ≈ 20.01 N

So, the answer is approximately 20.01 N.