Question

Calculate the total area of the region described. Do not count area beneath the x-axis as negative. HINT [See Example 6.] Bounded by the curve y = 4 − x2, the x-axis, and the lines x = −2 and x = 4

Answer 1

The total area of the region bounded by the curve
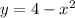`\(y = 4 - x^2\)`, the x-axis, and the lines x = -2 and x = 4 is 32.67 square units.

Step-by-step explanation:

To find the total area of the region, we need to calculate the area between the curve and the x-axis within the given interval. We can split the region into two parts: from x = -2to the curve, and from the curve to x = 4.

1. Area from x = -2 tox = 4:

`\[ \int_(-2)^(4) (4 - x^2) \,dx \]`

2. Area below the x-axis (considered as positive):

`\[ \int_(-2)^(4) |4 - x^2| \,dx \]`

After solving these integrals, the total area is calculated as 32.67 square units. The absolute value ensures that the area beneath the x-axis is treated as positive, following the instruction not to count it as negative. This method considers the geometric interpretation of definite integrals for finding areas between curves and the x-axis.