Answer:

Explanation:
The first thing we want to do is convert (x,y,z) to (r,θ,z):

With that out of the way, we need our bounds for each variable.
The variable
 is pretty easy since our region is a portion of a sphere, so with a circular cross-section, the bounds are
is pretty easy since our region is a portion of a sphere, so with a circular cross-section, the bounds are
 .
.
Now, we find the bounds for
 given the plane
given the plane
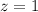 :
:
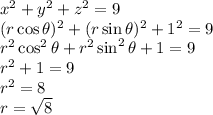
Therefore, the bounds for
 are
are
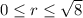 thanks to the bounds from
thanks to the bounds from
 earlier.
earlier.
Lastly, with
 , we want to write it in terms of
, we want to write it in terms of
 and get the bounds:
and get the bounds:
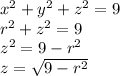
The radical is positive since the region is above the plane.
Now, we can form our triple integral and evaluate it:
![\displaystyle \int^(2\pi)_0\int_0^(√(8))\int_1^(√(9-r^2))r\,dz\,dr\,d\theta\\\\=\int^(2\pi)_0\int_0^(√(8))(r√(9-r^2)-r)\,dr\,d\theta\\\\=\int^(2\pi)_0d\theta\,\cdot\biggr[\int^(√(8))_0r√(9-r^2)\,dr-\int^(√(8))_0r\,dr\biggr]\\\\=2\pi\biggr[\int^(√(8))_0r√(9-r^2)\,dr-4\biggr]\\\\=2\pi\int_0^(√(8))r√(9-r^2)\,dr-8\pi](https://img.qammunity.org/2024/formulas/mathematics/high-school/wrxek8k2bwzyac8q3n231cfkgndmux8bfk.png)
Let
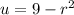 and
and
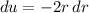 . Bounds now become
. Bounds now become
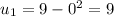 to
to
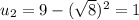 :
:
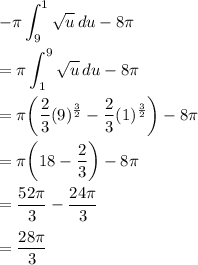
Therefore, the volume of the region is
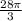 cubic units.
cubic units.