Question

Sketch the region enclosed by the given curves.

y = |10x|, y = x2 − 11

Answer 1

The region enclosed by the given curves is a combination of two separate regions: a triangular region above the x-axis formed by
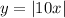`y = |10x|\)`, and a parabolic region below the x-axis formed by
`\(y = x^2 - 11\)`.

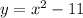Step-by-step explanation:

The first curve
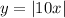`\(y = |10x|\)` represents a V-shaped graph symmetric about the y-axis, where the arms of the V open upwards. The absolute value function ensures that the graph is always positive. For
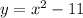`\(y = x^2 - 11\)`, a parabola opens upwards and is translated downward by 11 units. The intersection points between these two curves occur where
`\(|10x| = x^2 - 11\).` To find these points, we can set
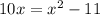`\(10x = x^2 - 11\)` and solve for x.

Once the intersection points are determined, the region enclosed by the curves can be found by evaluating
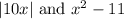`\(|10x|\) and \(x^2 - 11\)` within the bounds of these intersection points. The V-shaped graph of |10x| contributes to the region above the x-axis, while the parabola
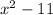`\(x^2 - 11\)` forms the region below the x-axis. Combining these regions results in the final enclosed area. It's crucial to consider the points of intersection, as they define the boundaries for evaluating the regions enclosed by the given curves.