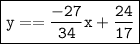Question

Find an equation of a line that passes throught (-2,3) and the point of intersesion of the lines x+2y=0 and 2x-y-12=0

find the equation of the line

Answer 1

The equation of the required line is:

`\boxed{ \tt y= =( -27)/(34)x+ (24)/(17)}`

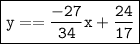
Explanation:

The point of intersection of the lines x+2y=0 and 2x-y-12=0 can be found by solving the system of equations.

x + 2y = 0

x=-2y .....(I)

2x - y - 12 = 0......(ii)

Substituting value of x in equation ii.

2(-2y)-y-12=0

-4y-y=12

-5y=12

`\tt y=- (12)/(5)`

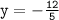
substituting value of y in equation I.

`x =-2*- (12)/(5)`

`x = (24)/(5)`

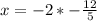
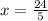
The slope of the line that passes through the points (-2, 3) and
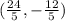`((24)/(5),-(12)/(5))` can be found using the formula:

`m =( (y_2 - y_1))/((x_2 - x_1))`

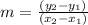
In this case, we have:

`\tt m (= ((-12/)/(5) - 3) )/(((24)/(5 )- (-2)))`

`\tt m =(((-12-3*5)/(5)))/(((24+2*5)/(5)))`

`m =( -27)/(34)`

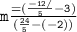
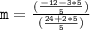
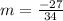
The point-slope form of a linear equation is:

`\tt y - y_1 = m(x - x_1)`

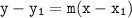
Using the point (-2,3) and the slope
`( -27)/(34)`

`\tt y-3 =( -27)/(34)(x-(-2))`)

`\tt y-3 =( -27)/(34)x+ ( -27)/(34)*2`

`\tt y= =( -27)/(34)x+ ( -27)/(17)+3`

`\tt y= =( -27)/(34)x+ ( -27+3*17)/(17)`

`\tt y= =( -27)/(34)x+ (24)/(17)`

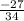
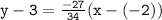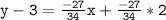
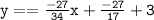
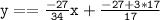
Therefore, the equation of the line that passes through (-2,3) and the point of intersection of the lines x + 2y = 0 and 2x - y - 12 = 0 is:

`\boxed{ \tt y= =( -27)/(34)x+ (24)/(17)}`