Question

A rigid tank contains 3.2 kg of water at 140

∘
C and 400kPa. Now 48 kJ of shaft work is done on the system and the final temperature in the tank is 80
∘
C. If the entropy change of water is zero and the surroundings are at 15
∘
C, determine (a) the final pressure in the tank, (b) the amount of heat transfer between the tank and the surroundings, and (c) the entropy generation during this process. Answers: (a) 47.4kPa, (b) 163 kJ, (c) 0.565 kJ/K

Answer 1

(a) Final pressure,
`$P_2 \approx 47.4 \mathrm{kPa}$`

(b) Heat transfer,
`$Q \approx 163 \mathrm{~kJ}$`

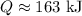
(c) Entropy generation,
`$\Delta S_{\text {gen }} \approx 0.565 \mathrm{~kJ} / \mathrm{K}$`

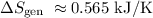
a) The final pressure in the tank can be determined by using the steam tables to determine the properties of the saturated liquid at the initial state and for the compressed liquid at the final state.

`\left.\begin{array}{l}T_1=140^(\circ) \mathrm{C} \\x_1=0 \text { (sat. liquid) }\end{array}\right\} \begin{aligned}& u_1=588.76 \mathrm{~kJ} / \mathrm{kg} \\& s_1=1.7392 \mathrm{~kJ} / \mathrm{kg} \cdot \mathrm{K}\end{aligned}`

Since we want a zero entropy change,
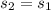`s_2=s_1` and therefore the final state properties are:

`\left.\begin{array}{l}T_2=80^(\circ) \mathrm{C} \\s_2=s_1=1.7392 \mathrm{~kJ} / \mathrm{kg} \cdot \mathrm{K}\end{array}\right\} \begin{aligned}& P_2=47.4 \mathrm{kPa} \\& u_2=552.93 \mathrm{~kJ} / \mathrm{kg}\end{aligned}`

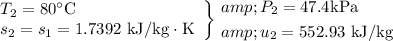
b) The heat transfer between the tank and the surroundings can be determined from and energy balance on the system, with the contents of the tank being the system:

`\begin{array}{rlr}\Delta E_{\text {system }} & = E_{\text {in }}-E_{\text {out }} \\\Delta U & = W_{\mathrm{Pw}_{\text {in }}}-Q_{\text {out }} \\Q_{\text {out }} & = W_{\mathrm{Pw}, \text { in }}-m\left(u_2-u_1\right) \\Q_{\text {out }} & =48 \mathrm{~kJ}-(3.2 \mathrm{~kg})(552.93-588.76) \mathrm{kJ} / \mathrm{kg} \\& = 163 \mathrm{~kJ}\end{array}`

c) The entropy generation for this process will only be the result of the entropy change of the surroundings, since the entropy change of water is zero. This gives:

`S_{\text {gen }}=\Delta S_{\text {surr }}=\frac{Q_{\text {out }}}{T_{\text {surr }}}=\frac{163 \mathrm{~kJ}}{(15+273) \mathrm{K}}=0.565 \frac{\mathrm{kJ}}{\mathrm{kg}}`