Question

Mattress Kingdom produces two types of mattresses, king and queen. The cost of producing x king and y queen mattresses is modeled by the equation

C(x,y)=3x^2−xy+6y^2+4
A retail store recently placed an order for a total of 90 mattresses. How many of each type should Mattress Kingdom produce to fulfill the order AND minimize their production cost?

a)53 king and 37 queen

b)58 king and 32 queen

c)31 king and 59 queen

d)37 king and 53 queen

Answer 1

a) 54 king and 36 queen

Step-by-step explanation:

Given, Modeled equation as
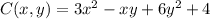`C(x,y)=3x^2-xy+6y^2+4` and

As given in the question King mattress =
`x` and queen mattress =
`y`

and
`x+y=90= > y=90-x` (eqn.1)

The mattress equation is modified as follows,

`= > C=3x^2-x(90-x)+6(90-x)^2+4\\= > C=3x^2-90x+x^2+6[(90)^2+(x)^2-2(90)x]+4`

Now differentiate the equation w.r.t x we get i.e..,
`dc/dx=0\\`

`= > 6x+2x-90+12x-12(90)=0\\= > 20(x)-12(90)=0\\= > 20(x)=12(90)\\= > x=54`

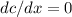
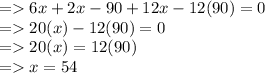
according to the eqn.1, we get..,

`= > y=90-x\\= > y=90-54\\= > y=36`

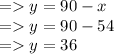
Therefore, 54 king-size mattresses and 36 queen-size mattresses are required to minimize the cost