Answer:
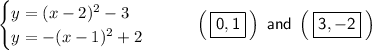
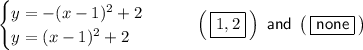
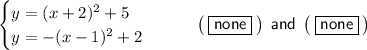
Explanation:
The points where the graphs of the equations intersect are the solutions to a graphed system of equations.
Therefore, to determine the number of solutions to the given graphed systems of equations, observe the number of points of intersection between the graphs.

Given system of equations:
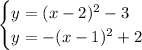
From observation of the given graph of this system of equations, there are 2 points of intersection, so there are 2 solutions.
The 2 solutions are:

Given system of equations:
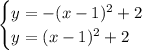
From observation of the given graph of this system of equations, there is one point of intersection, so there is one solution.
The solution is:

Given system of equations:
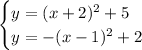
From observation of the given graph of this system of equations, there are no points of intersection, so there are no solutions.