Answer:
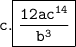
Explanation:

Distribute the exponents.
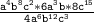
Combining like terms.

Cancel out common factors.
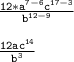
Therefore, the simplified expression is
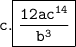
Note:
For rule of indices:
There are the 7 laws of indices:
1. Power of a power:
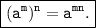
2. Product of powers:
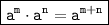
3. Quotient of powers:
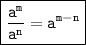
4. Power of a product:

5. Power of a quotient:
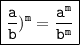
6. Zeroth power:
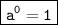 , for any non-zero real number a.
, for any non-zero real number a.
7. Negative power:
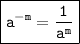 , for any non-zero real number a and positive integer m.
, for any non-zero real number a and positive integer m.