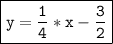Slope intercept form of y+1=1/4(x-2)

Question

asked Dec 16, 2024 7.4k views

2 Answers

Merna · Answer 1 · 2024-12-18T19:44:18+0000

Answer:

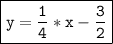
$\boxed{ \tt y=(1)/(4)*x - (3)/(2)}$

Explanation:

First, we can distribute the
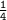$\tt (1)/(4)$ on the right side of the equation:

$\tt y+1 = (1)/(4)(x-2)$

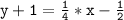
$\tt y+1 = (1)/(4)*x - (1)/(2)$

Then, we can subtract 1 from both sides of the equation to get y by itself:

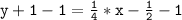
$\tt y+1 - 1 =(1)/(4)*x - (1)/(2)- 1$

$\tt y =(1)/(4)*x -( (1)/(2))$

Finally, we can combine the constant terms on the right side of the equation to get the slope intercept form:

$\tt y=(1)/(4)*x - (1+2)/(2)$

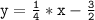
$\tt y=(1)/(4)*x - (3)/(2)$

Therefore, slope intercept form=
$\boxed{ \tt y=(1)/(4)*x - (3)/(2)}$

Maroodb · Answer 2 · 2024-12-20T02:47:16+0000

Answer:

y=(1)/(4)x-(3)/(2)

Explanation:

The slope-intercept form of a linear equation is y = mx + b, where m represents the slope and b represents the y-intercept.

Given linear equation:

y+1=(1)/(4)(x-2)

To rewrite the given linear equation in slope-intercept form, begin by distributing the parentheses on the right side of the equation:

y+1=(1)/(4)x-(2)/(4)

y+1=(1)/(4)x-(1)/(2)

Subtract 1 from both sides of the equation to isolate y:

y+1-1=(1)/(4)x-(1)/(2)-1

y=(1)/(4)x-(3)/(2)

Therefore, the slope-intercept form of the given equation is:

$\large \boxed{\boxed{y=(1)/(4)x-(3)/(2)}}$