Question

Help For each of the systems and graphs given, identify the solution(s). Remember to use the format (x,y)

to type in your points, and do not use spaces. If there is only one, type the point in one space and “none” in the other. If there is none, type none in both the boxes.

Answer 1

`\begin{cases}y=x+5\\y=-(x-1)^2+2\end{cases}\qquad \left(\:\boxed{\sf none}\:\right)\; \sf and \; \left(\:\boxed{\sf none}\:\right)`

`\begin{cases}y=-x-3\\y=-(x-1)^2+2\end{cases} \qquad \left(\:\boxed{-1, -2}\:\right)\; \sf and \; \left(\:\boxed{4, -7}\:\right)`

`\begin{cases}y=-(x-1)^2+2\\y=2\end{cases}\qquad \left(\:\boxed{1,2}\:\right)\; \sf and \; \left(\:\boxed{\sf none}\:\right)`

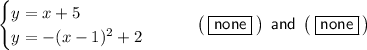
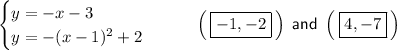
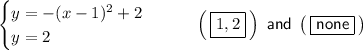
Explanation:

The solutions to a graphed system of equations can be found at the points where the graphs of the equations intersect.

`\hrulefill`

Given system of equations:

`\begin{cases}y=x+5\\y=-(x-1)^2+2\end{cases}`

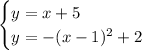
From observation of the given graph of this system of equations, there are no solutions, as there are no points of intersection.

`\hrulefill`

Given system of equations:

`\begin{cases}y=-x-3\\y=-(x-1)^2+2\end{cases}`

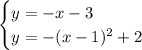
For this graphed system of equations, there are 2 solutions as there are 2 points of intersection.

From observation of the given graph, the points of intersection are:

• (-1, -2) and (4, -7)

`\hrulefill`

Given system of equations:

`\begin{cases}y=-(x-1)^2+2\\y=2\end{cases}`

For this graphed system of equations, there is one solution as there is one point of intersection.

From observation of the given graph, the point of intersection is:

• (1, 2)