Question

VWXY is a rhombus. Find mzVYX.

6m-12
(9n+ 4)º
Z
¹X
W
4m + 4
(3n²-0.75)

Answer 1

To find mzVYX, we need to understand the properties of a rhombus.

In a rhombus, opposite angles are congruent, which means they have the same measure. Since VWXY is a rhombus, angle V and angle Y must be congruent.

From the given options, the only option that represents congruent angles is (9n+4)º. So, mzVYX is equal to (9n+4)º.

To summarize:

mzVYX = (9n+4)º

Answer 2

∠ VYX = 73°

Explanation:

in a rhombus

• the diagonals are perpendicular bisectors of each other

then ∠ WZX = 90° , so

3n² - 0.75 = 90 ( add 0.75 to both sides )

3n² = 90.75 ( divide both sides by 3 )

n² = 30.25 ( take square root of both sides )

n =
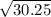`√(30.25)` = 5.5

• the diagonals bisect the angles

then

∠ YVW = 9n + 4 = 9n + 4 = 18n + 8 = 18(5.5) + 8 = 99 + 8 = 107°

• consecutive angles are supplementary

so

∠ VYX + ∠ YVW = 180°

∠ VYX + 107° = 180° ( subtract 107° from both sides )

∠ VYX = 73°