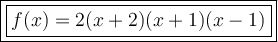Question

Express the polynomial as a product of linear factors.

f(x) = 2x ^ 3 + 4x ^ 2 - 2x - 4

A. (x - 4)(x + 1)(x - 1)

B. (x - 2)(x - 2)(x - 1)

OC. 2(x + 2)(x + 1)(x - 1)

D. (x - 2)(x + 1)(x - 1)

Answer 1

The polynomial f(x) = 2x^3 + 4x^2 - 2x - 4 can be expressed as a product of linear factors as:

f(x) = 2(x + 2)(x - 1)(x - 1)

Therefore, the correct option is C. 2(x + 2)(x + 1)(x - 1).

Answer 2

`\textsf{C.}\quad 2(x + 2)(x + 1)(x - 1)`

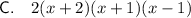
Explanation:

Given polynomial function:

`f(x) = 2x^3 + 4x^2 - 2x - 4`

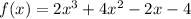
Each answer option has (x - 1) as a factor.

Therefore, (x - 1) must be a factor of the given polynomial.

To double-check this, we can use the Factor Theorem.

The Factor Theorem states that if f(x) is a polynomial, and f(a) = 0, then (x - a) is a factor of f(x).

Therefore, if (x - 1) is a factor of f(x), then we would expect f(1) = 0:

`\begin{aligned}f(1) &= 2(1)^3 + 4(1)^2 - 2(1) - 4\\&=2+4-2-4\\&=0 \end{aligned}`

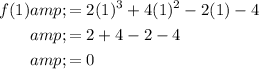
Therefore, this confirms that (x - 1) is a factor of the given polynomial.

Divide the polynomial by the found linear factor using the method of long division:

`\large \begin{array}{r}2x^2+6x+4\phantom{)}\\x-1{\overline{\smash{\big)}\,2x^3+4x^2-2x-4\phantom{)}}}\\{-~\phantom{(}\underline{(2x^3-2x^2)\phantom{-bwww.)}}\\6x^2-2x-4\phantom{)}\\-~\phantom{()}\underline{(6x^2-6x)\phantom{ww.}}\\4x-4\phantom{)}\\-~\phantom{()}\underline{(4x-4)\phantom{}}\\0\phantom{)}\end{array}`

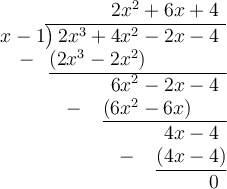
Therefore:

`f(x) = (x-1)(2x^2+6x+4)`

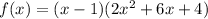
Factor out 2 from the quadratic factor:

`f(x) = 2(x-1)(x^2+3x+2)`

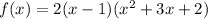
Factor the quadratic:

`\begin{aligned}x^2+3x+2&=x^2+x+2x+2\\&=x(x+1)+2(x+1)\\&=(x+1)(x+2)\end{aligned}`

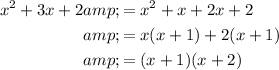
Therefore, the fully factored polynomial is:

`f(x) = 2(x-1)(x+1)(x+2)`

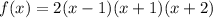
Rearrange the factors to give:

`\large\boxed{\boxed{f(x) = 2(x+2)(x+1)(x-1)}}`