Question

in a circle an arc of length 110cm subtends an angle of 210° at the center. find the radius of the circle ( table π=²²/⁷⁷​

Answer 1

r ≈ 30 cm

Explanation:

the arc length of a circle is calculated as

arc = circumference of circle × fraction of circle

= 2πr ×
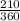`(210)/(360)` ( r is the radius )

here arc = 110 , then

2πr ×
`(21)/(36)` = 110

2πr ×
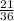`(7)/(12)` = 110 ( multiply both sides by 12 to clear the fraction )

14πr = 1320 ( divide both sides by 14π )

r =
`(1320)/(14\pi )` ≈ 30 cm ( to the nearest whole number )

Answer 2

r = 30 cm

Explanation:

To find the radius of the circle, given the central angle and arc length, we can use the arc length formula:

`\boxed{\begin{array}{l}\underline{\sf Arc\;length}\\\\\textsf{Arc length}= \pi r\left((\theta)/(180^(\circ))\right)\\\\\textsf{where:}\\ \phantom{ww}\;\bullet\;r\;\textsf{is the radius.} \\ \phantom{ww}\;\bullet\;\theta\;\textsf{is the angle measured in degrees.}\\\end{array}}`

Given values:

• θ = 210°
• Arc length = 110 cm
• π = 22/7

Substitute the given values into the formula and solve for r:

`\begin{aligned}\sf Arc \; length &= \pi r\left((\theta)/(180^(\circ))\right)\\\\110&=(22)/(7) r\left((210^(\circ))/(180^(\circ))\right)\\\\110&=(22)/(7) r\left((7)/(6)\right)\\\\110&=(22)/(6) r\\\\110&=(11)/(3) r\\\\110 \cdot 3&=(11)/(3) r \cdot 3\\\\330&=11r\\\\(330)/(11)&=(11r)/(11)\\\\30&=r\\\\r&=30\; \sf cm\end{aligned}`

Therefore, the radius of the circle is 30 cm.