Question

in exercises 26-28, find the shaded area to the nearest 0.1 cm^2. In exercises 27 and 28, the quadrilateral is a square and all arcs are arcs of a circle of radius 6 cm. Solve for the SHADED area in each problem.

Answer 1

26) 153.9 cm²

27) 72 cm²

28) 30.9 cm²

Explanation:

Question 26

The diagram shows a semicircle with a diameter of 28 cm with two smaller congruent semicircles cut out of it. The diameter of each smaller circle is half the diameter of the larger circle.

To find the shaded area, subtract the areas of the smaller semicircles from the area of the larger semicircle.

The formula for the area of a semicircle is:

`\boxed{\sf Area_(\sf semicircle)=(1)/(2) \pi r^2}`

where r is the radius of the semicircle.

Since the radius of a semicircle is half its diameter:

• The radius of the larger semicircle is 14 cm.
• The radius of the smaller semicircle is 7 cm.

Therefore, the shaded area can be calculated as:

`\begin{aligned}\sf Shaded\;area&=\sf Larger\;semicircle-2\;Smaller\;semicircles\\\\&=(1)/(2) \pi (14)^2-2 \cdot (1)/(2) \pi (7)^2\\\\&=(1)/(2) \pi \cdot196 -\pi \cdot 49\\\\&=98\pi - 49\pi\\\\&=49 \pi\\\\&=153.93804...\\\\&=153.9\; \sf cm^2\end{aligned}`

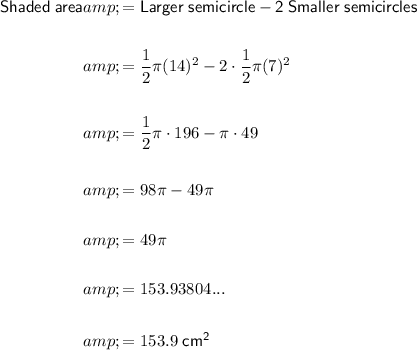
Therefore, the shaded area is 153.9 cm², rounded to the nearest tenth.

`\hrulefill`

Question 27

The diagram shows a square with a quarter-circle arc of radius 6 cm in each corner. Therefore, each side length of the square is equal to two radii, so s = 12 cm.

If we divide the square into 4 equal quadrants (see first attachment), we can see that the quarter-circle sectors subtracted from the upper left and bottom right quadrants, are congruent to the shaded quarter-circle sectors of the upper right and lower left quadrants.

Therefore, the shaded part is equal to half the area of the square.

The area of a square is the square of its side length.

Therefore, the area of the shaded part can be found by halving the area of the square:

`\begin{aligned}\sf Shaded\;area&=(1)/(2)s^2\\\\&=(1)/(2) (12)^2\\\\&=(1)/(2) \cdot 144\\\\&=72\; \sf cm^2\end{aligned}`

Therefore, the shaded area is 72 cm².

`\hrulefill`

Question 27

The diagram shows a square with a quarter-circle arc of radius 6 cm in each corner. Therefore, each side length of the square is equal to two radii, so s = 12 cm.

If we divide the square into 4 equal quadrants (see second attachment) we can see that 4 congruent quarter-circle sectors have been subtracted from the square. Since the sum of 4 quarter-circles is a whole circle, the shaded area can be calculated by subtracting the area of a circle with radius 6 cm from the area of the square.

Therefore, the shaded area can be calculated as:

`\begin{aligned}\sf Shaded\;area&=\sf Square-Circle\\\\&=s^2-\pi r^2\\\\&=12^2-\pi (6)^2\\\\&-144-36\pi\\\\&=30.90266447....\\\\&=30.9\; \sf cm^2\end{aligned}`

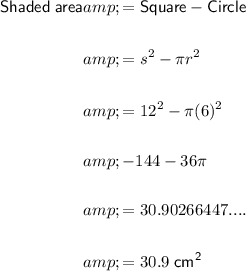
Therefore, the shaded area is 30.9 cm², rounded to the nearest tenth.