Question

Dy

dx
Assume x and y are functions of t. Evaluate - for 3xy-4x+4y³ = -32, with the conditions = -8, x= 4, y = -1.
dt
dt
55
(Type an exact answer in simplified form.)

Answer 1

To evaluate the derivative of the given expression with respect to time, we use implicit differentiation.

Differentiating both sides of the equation with respect to time t, we get:

3x(dy/dt) + 3y(dx/dt) - 4(dx/dt) + 12y²(dy/dt) = 0

Rearranging the terms, we get:

(3xy + 12y²)(dy/dt) + (3y - 4)(dx/dt) = 0

Substituting the given values, we get:

(3 * 4 * (-1) + 12(-1)²)(dy/dt) + (3(-1) - 4)(-8) = 0

Simplifying, we get:

-9(dy/dt) + 28 = 0

Solving for dy/dt, we get:

dy/dt = 28/9

Therefore, the exact answer in simplified form is:

dy/dt = 28/9.

Answer 2

`\frac{\text{d}y}{\text{d}t}=-(7)/(3)`

Explanation:

To find dy/dt given dx/dt, we need to first find dy/dx, since:

`\frac{\text{d}y}{\text{d}t}=\frac{\text{d}y}{\text{d}x} * \frac{\text{d}x}{\text{d}t}`

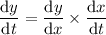
To find dy/dx, differentiate the given equation that contains a mixture of x and y terms with respect to x using implicit differentiation.

Begin by placing d/dx in front of each term of the equation:

`\frac{\text{d}}{\text{d}x}3xy-\frac{\text{d}}{\text{d}x}4x+\frac{\text{d}}{\text{d}x}4y^3=\frac{\text{d}}{\text{d}x}(-32)`

Differentiate the terms in x only (and constant terms):

`\frac{\text{d}}{\text{d}x}3xy-4+\frac{\text{d}}{\text{d}x}4y^3=0`

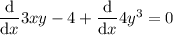
Use the chain rule to differentiate terms in y only.

In practice, this means differentiate with respect to y, and place dy/dx at the end:

`\frac{\text{d}}{\text{d}x}3xy-4+12y^2\frac{\text{d}y}{\text{d}x}=0`

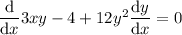
Use the product rule to differentiate the term in x and y.

`3x\frac{\text{d}y}{\text{d}x}+3y-4+12y^2\frac{\text{d}y}{\text{d}x}=0`

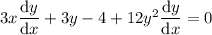
Rearrange the resulting equation to isolate dy/dx:

`3x\frac{\text{d}y}{\text{d}x}+12y^2\frac{\text{d}y}{\text{d}x}+3y-4=0`

`(3x+12y^2)\frac{\text{d}y}{\text{d}x}+3y-4=0`

`(3x+12y^2)\frac{\text{d}y}{\text{d}x}=4-3y`

`\frac{\text{d}y}{\text{d}x}=(4-3y)/(3x+12y^2)`

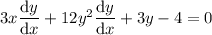
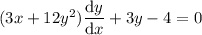
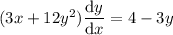
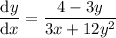
Now we have found dy/dx, and given that dx/dt = -8, we can create an expression for dy/dt:

`\frac{\text{d}y}{\text{d}t}=\frac{\text{d}y}{\text{d}x} * \frac{\text{d}x}{\text{d}t}`

`\frac{\text{d}y}{\text{d}t}=(4-3y)/(3x+12y^2) * (-8)`

`\frac{\text{d}y}{\text{d}t}=(-8(4-3y))/(3x+12y^2)`

`\frac{\text{d}y}{\text{d}t}=(24y-32)/(3x+12y^2)`

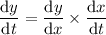
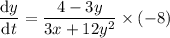
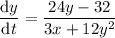
To find the value of dy/dt when x = 4 and y = -1, substitute these values into the found expression for dy/dt:

`\frac{\text{d}y}{\text{d}t}=(24(-1)-32)/(3(4)+12(-1)^2)`

`\frac{\text{d}y}{\text{d}t}=(-24-32)/(12+12)`

`\frac{\text{d}y}{\text{d}t}=(-56)/(24)`

`\frac{\text{d}y}{\text{d}t}=-(7)/(3)`

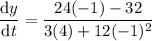
Therefore, the value of dy/dt for the given conditions is -7/3.