Question

The radius of a spherical balloon is increasing at the rate of 0.8 cm/minute. How fast is the volume changing when the

radius is 7.9 cm?
The volume is changing at a rate of cm³/minute.
(Type an integer or a decimal. Round to one decimal place as needed.)

Answer 1

627.4 cm³/minute

Explanation:

We want to find how fast the volume of a spherical balloon is changing when its radius is defined.

Let V be the volume of the spherical balloon (in cm³).

Let r be the radius of the spherical balloon (in cm).

Let t be the time (in minutes).

To find the rate of change of volume V (with respect to time t), we need to find the equation for dV/dt.

`\hrulefill`

Given the radius of a spherical balloon is increasing at the rate of 0.8 cm/minutes then:

`\frac{\text{d}r}{\text{d}t}=0.8`

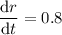
The formula for the volume of a sphere is:

`V=(4)/(3)\pi r^3`

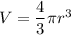
Find dV/dr by differentiating V with respect to r:

`\frac{\text{d}V}{\text{d}t}=3 \cdot (4)/(3) \pi r^(3-1)`

`\frac{\text{d}V}{\text{d}r}=4 \pi r^(2)`

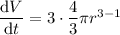
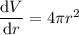
Now we have expressions for dr/dt and dV/dr, we can multiply them to find the equation for dV/dt:

`\frac{\text{d}V}{\text{d}t}=\frac{\text{d}V}{\text{d}r} * \frac{\text{d}r}{\text{d}t}`

`\frac{\text{d}V}{\text{d}t}=4 \pi r^(2) * 0.8`

`\frac{\text{d}V}{\text{d}t}=3.2 \pi r^(2)`

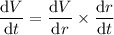
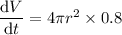
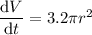
To calculate how fast the volume is changing when the radius is 7.9 cm, substitute r = 7.9 into the found equation for dV/dt:

`\frac{\text{d}V}{\text{d}t}=3.2 \pi (7.9)^(2)`

`\frac{\text{d}V}{\text{d}t}=3.2 \pi (62.41)`

`\frac{\text{d}V}{\text{d}t}=199.712 \pi`

`\frac{\text{d}V}{\text{d}t}=627.41375...`

`\frac{\text{d}V}{\text{d}t}=627.4\; \sf cm^3/min`

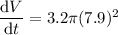
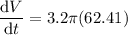
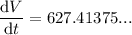
Therefore, the volume of the spherical balloon is changing at a rate of 627.4 cm³/minute when its radius is 7.9 cm.