Question

Find the energy of the following. Express your answers in units of electron volts, noting that 1 eV = 1.60 10-19 J.

(a) a photon having a frequency of 5.60 1017 Hz


(b) a photon having a wavelength of 2.60 102 nm

Answer 1

a) The energy of the photon is 2.3210³ eV.

b) The photon energy is 4.7610⁵ eV.

To find the energy of a photon, we can use the following formula:

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{E=hf} \end{gathered}$} }`

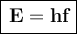
Where

• E is the energy
• h is planck's constant
• f is the frequency

a) If the frequency of the button is 5.60 10¹⁷ Hz, then its energy is:

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{E=hf} \end{gathered}$} }`

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{E=(6.6310^(-34)\:J\cdot s)(5.6070^(17)Hz) } \end{gathered}$} }`

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{E=3.7110^(-16) \ J} \end{gathered}$} }`

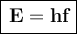
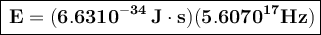
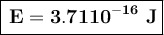
To convert this energy to units of electron volts, we divide by the value of electron volts:

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{E= (3.7110^(-16) \ J)/(1.6010^(-19) \ J/eV) } \end{gathered}$} }`

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{E=2.3210^3 \ eV} \end{gathered}$} }`

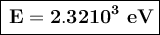
The energy of the photon is 2.3210³ eV.

b). If the wavelength is 2.6010^-2 nm, then we can use the relationship between wavelength and frequency.

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{f=(c)/(\lambda) } \end{gathered}$} }`

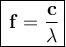
Where:

• C is the speed of light
• λ is the wavelength

The frequency of the photon is then:

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{f=(c)/(\lambda) } \end{gathered}$} }`

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{f=(3.0010^8 \ m/s)/(2.6010^(-12) \ m) } \end{gathered}$} }`

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{f=1.1510^(20) \ Hz } \end{gathered}$} }`

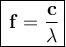
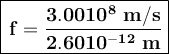
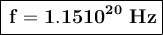
Using the energy formula we have, we have:

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{E=hf} \end{gathered}$} }`

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{E=(6.6310^(-34)\:J\cdot s)(1.1510^(20)\:Hz)} \end{gathered}$} }`

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{E=7.6210^(-14) \ J} \end{gathered}$} }`

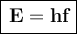
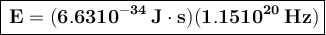
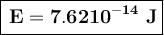
To convert this energy to units of electron volts, we divide by the value of electron volts:

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{E=(7.6210^(-14) \ J )/(1.6010^(-19) \ J/eV ) } \end{gathered}$} }`

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{E=4.7610^5 \ eV } \end{gathered}$} }`

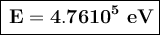
The photon energy is 4.7610⁵ eV.