Answer:
Width = 6.5 ft
Length = 10 ft
Explanation:
- We can allow the variables w and l to represent the width and length of the rectangle.
- The formula for the area of a rectangle is given by:
A = lw, where
- A is the area in units squared,
- l is the length,
- and w is the width.
Since the area of the rectangle is 65 ft^2, so we can use the following equation to represent the are:
l * w = 65
Since we're also told that the length is 3 ft less than twice the width, we can represent this with the following equation:
l = 2w - 3.
Substituting the expression for l from the second equation into the first equation gives us:
(2w - 3) * w = 65
Expanding this expression gives us:
2w^2 - 3w = 65
Subtracting 65 from both sides gives us:
2w^2 - 3w - 65 = 0
We can solve this quadratic equation for w using the quadratic formula:
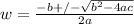
Plugging these values into the formula gives us:
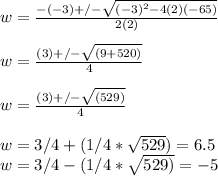
We can't have a negative dimension so the width is 6.5 ft.
Now we can plug in 6.5 for w and 65 for A in the rectangle area formula to find l, the length of the rectangle:
(65 = 6.5l) / 6.5
10 = l
Thus, the length is 10 ft.