Question

A rock is thrown into a still pond. The circular ripples move outward from the point of impact of the rock so that the radius

of the circle formed by a ripple increases at the rate of 3 feet per second. Find the rate at which the area is changing at
the instant the radius is 15 feet.
When the radius is 15 feet, the area is changing at approximately
(Round to the nearest thousandth as needed.)
square feet per second.

Answer 1

282.743 square feet per second

Explanation:

We are told that a rock is thrown into a still pond, and that circular ripples move outward from the point of impact of the rock.

We want to find the rate at which the circular area formed by a ripple is changing when its radius is defined.

Let A be the area of the circle (in ft²).

Let r be the radius of the circle (in ft).

Let t be the time (in seconds).

Therefore, to find the rate of change of area A (with respect to time t), we need to find the equation for dA/dt.

`\hrulefill`

Given the circular ripples move outward from the point of impact of the rock so that the radius of the circle formed by a ripple increases at the rate of 3 ft/s, then:

`\frac{\text{d}r}{\text{d}t}=3`

The formula for the area of a circle is A = πr².

Find dA/dr by differentiating A with respect to r:

`\frac{\text{d}A}{\text{d}r}=2 \cdot \pi r^(2-1)`

`\frac{\text{d}A}{\text{d}r}=2 \pi r`

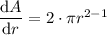
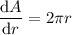
Now we have expressions for dr/dt and dA/dr, we can multiply them to find the equation for dA/dt:

`\frac{\text{d}A}{\text{d}t}=\frac{\text{d}A}{\text{d}r} * \frac{\text{d}r}{\text{d}t}`

`\frac{\text{d}A}{\text{d}t}=2\pi r * 3`

`\frac{\text{d}A}{\text{d}t}=6\pi r`

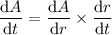
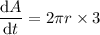
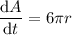
To calculate how fast the circular area is changing when the radius is 15 feet, substitute r = 15 into the found equation for dA/dt:

`\frac{\text{d}A}{\text{d}t}=6\pi (15)`

`\frac{\text{d}A}{\text{d}t}=90\pi`

`\frac{\text{d}A}{\text{d}t}=282.743338...`

`\frac{\text{d}A}{\text{d}t}=282.743\; \sf ft^2/s`

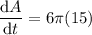
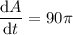
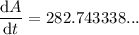
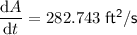
Therefore, when the radius is 15 feet, the area is changing at approximately 282.743 square feet per second (rounded to the nearest thousandth).