Question

Calculate the work done to stretch an elastic spring by 40cm. If a force of 10N produces an extension of 4cm in it. U

Answer 1

`20\; {\rm J}`.

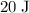Step-by-step explanation:

The question has given the force it takes to stretch this spring by a particular length. With that information, the amount of work completed in order to stretch this spring by a different length can be found using the following steps:

• Find the spring constant
  `k` of the spring from the restoring force and the corresponding displacement of the spring, and
• Apply the equation for the elastic potential energy
  `\text{EPE}` of ideal springs to find the energy required to stretch the spring by the given distance.

Note the unit conversion during the calculations- all values should be measured in standard units, with distances measured in meters.

To find the spring constant
`k` of an ideal spring, divide the restoring force by the change in the length of the spring.

`\displaystyle \text{spring constant} = \frac{\text{restoring force}}{\text{change in length}}`.

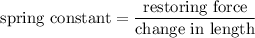In this question, it is given that an external force of
`10\; {\rm N}` is needed to increase the length of the spring by
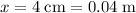`x = 4\; {\rm cm} = 0.04\; {\rm m}` (note the unit conversion.) In other words, the restoring force on the spring would be
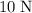`10\; {\rm N}\!` in response to a change in length of
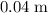`0.04\; {\rm m}`. The spring constant would be:

`\begin{aligned}k &= \frac{(\text{restoring force})}{(\text{change in length})} \\ &= \frac{10\; {\rm N}}{0.04\; {\rm m}} \\ &= 250\; {\rm N\cdot m^(-1)}\end{aligned}`.

For an ideal spring of spring constant
`k`, if the length of the spring is changed by
`x`, the elastic potential energy
`\text{EPE}` stored in that spring would be:

`\displaystyle \text{EPE} = (1)/(2)\, k\, x^(2)`.

The spring constant in this question is
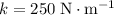`k = 250\; {\rm N\cdot m^(-1)}`, whereas the displacement of the spring needs to be
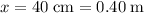`x = 40\; {\rm cm} = 0.40\; {\rm m}` (again, note the unit conversion.) The elastic potential energy stored in this spring would be:

`\begin{aligned} \text{EPE} &= (1)/(2)\, k\, x^(2) \\ &= (1)/(2)\, (250\; {\rm N\cdot m^(-1)})\, (0.40\; {\rm m})^(2) \\ &= 20\; {\rm N\cdot m} \\ &= 20\; {\rm J}\end{aligned}`.

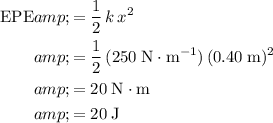(Note that
`1\; {\rm N\cdot m} = 1\; {\rm J}`.)

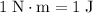In other words, when an external force stretches this spring by
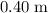`0.40\; {\rm m}` from the equilibrium position, the amount of work done on the spring would be
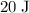`20\; {\rm J}`.