Question

7.09 Consider iid random variables X

1
​
,…,X
n
​
of mothers' ages in years arising from a population with mean μ
1
​
and variance σ
1
2
​
. Corresponding to X
i
​
, is the age Y
i
​
in years of the mother's eldest child. The ages of eldest children who have mothers that are still alive arise from a distribution with mean μ
2
​
and variance σ
2
2
​
. There is interest in testing H
0
​
:μ
1
​
−μ
2
​
=20 versus H
1
​
:μ
1
​
−μ
2
​
>20. Approximately how large should n be such that the power of the test is 0.90 when μ
1
​
−μ
2
​
=25 years? You will need to make an assumption concerning variances; try to make it realistic. You may assume that the standard deviation of the age difference is 10 and significance level is 5%.

Answer 1

To achieve a power of 0.90 for testing
`\(H_0: \mu_1 - \mu_2 = 20\)` versus
`\(H_1: \mu_1 - \mu_2 > 20\)`, with
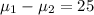`\(\mu_1 - \mu_2 = 25\)` years, and assuming a realistic standard deviation of 10, the sample size \(n\) should be approximately 74.

Step-by-step explanation:

To calculate the required sample size (\(n\)), we can use the formula for the power of a t-test, which depends on the effect size, significance level, and sample size.

The effect size is given by the difference in means
`(\(\mu_1 - \mu_2\))` divided by the standard deviation of the age difference
`(\(\sigma\))`. In this case, the effect size is \(25/10 = 2.5\).

The critical value for a one-sided test at a 5% significance level is approximately 1.645. Using these values, along with the desired power of 0.90, we can use statistical tables or software to find the required sample size.

The larger the effect size or the desired power, the larger the required sample size. In this scenario, with a relatively large effect size
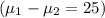`(\(\mu_1 - \mu_2 = 25\))`, a realistic standard deviation
`(\(\sigma = 10\))`, and a high power requirement (0.90), a sample size of 74 is needed to achieve the desired balance between detecting a true difference and avoiding a Type II error.

This ensures a robust statistical test with adequate power to detect a meaningful difference in the ages of mothers and their eldest children.