Question

IRECTIONS Answer the questions based on the data given below.

ote: Technology is recommended, but not required, for this activity.
Joey records how long it takes him (in minutes) to hike a mountain trail each day for 6 days.
50 52 58 55 59 50
Find the mean, standard deviation, and the five-number summary for Joey's data.

Answer 1

Mean = 54

Standard deviation = 3.61

Five-number summary:

• Minimum value = 50
• Lower Quartile (Q1) = 50
• Median (Q2) = 53.5
• Upper Quartile (Q3) = 58
• Maximum value = 59

Explanation:

Given data values:

• 50, 52, 58, 55, 59, 50

`\hrulefill`

Mean

To calculate the mean of a data set, divide the sum of the data values by the total number of data values. Therefore:

`\begin{aligned}\textsf{Mean,\;$\mu$}&=(50+ 52+ 58+ 55+ 59+ 50)/(6)\\\\&=(324)/(6)\\\\&=54\end{aligned}`

`\hrulefill`

Standard deviation

To calculate the standard deviation of a data set, divide the sum of the squares of the data values by the total number of data values, subtract the square of the mean, then square root the result. Therefore:

`\begin{aligned}\textsf{Standard\;deviation,\;$\sigma$}&=\sqrt{(\sum x^2)/(n)-\mu^2}\\\\&=\sqrt{(50^2+ 52^2+ 58^2+ 55^2+ 59^2+ 50^2)/(6)-54^2}\\\\&=\sqrt{(17574)/(6)-2916}\\\\&=√(2929-2916)\\\\&=√(13)\\\\&=3.61\; \sf (2\;d.p.)\end{aligned}`

`\hrulefill`

Five-number summary

The five-number summary is a descriptive statistical summary of a data set that consists of five key values:

• Minimum: The minimum data value.
• Lower Quartile (Q1): The median of the data points to the left of the median.
• Median (Q2): The middle value when all data values are placed in order of size.
• Upper Quartile (Q3): The median of the data points to the right of the median.
• Maximum: The maximum data value.

Order the given data values from smallest to largest:

• 50, 50, 52, 55, 58, 59

The minimum value is 50, and the maximum value is 59.

As the data set is an even data set, the median is the mean of the middle two values:

`\sf Median\;(Q2)=(55+52)/(2)=53.5`

The lower quartile is the median of the data points to the left of the median.

`\sf Lower \; Quartile\;(Q1)=50`

The upper quartile is the median of the data points to the right of the median.

`\sf Upper \;Quartile \;(Q3)= 58`

Therefore, the five-number summary of the given data set is:

• Minimum = 50
• Lower Quartile = 50
• Median = 53.5
• Upper Quartile = 58
• Maximum = 59

Answer 2

Mean =54

Standard Deviation: 3.605

Five number summary:

• Minimum: 50
• First quartile (Q1): 50
• Median:53.5
• Third quartile (Q3):58
• Maximum: 59

Explanation:

Given:

Trail each day for 6 days.

50 52 58 55 59 50

Mean is calculated by adding up all the data points and dividing by the number of data points (6).

`\tt Mean= (50 + 52 + 58 + 55 + 59 + 50)/(6) = (324)/(6)=54`

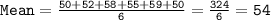
Sum =324 and Mean =54

Again,

`\hrulefill`

For Standard Deviation:

To find the standard deviation, we need to find the differences between each data point and the mean, square those differences, calculate the mean of the squared differences, and finally take the square root of that mean.

First, calculate the differences between each data point and the mean:

(50 - 54)² = 16

(52 - 54)² = 4

(58 - 54)² = 16

(55 - 54)² = 1

(59 - 54)² = 25

(50 - 54)² = 16

Next, calculate the mean of the squared differences:

`((16 + 4 + 16 + 1 + 25 + 16) )/(6) = (78)/(6)=13`

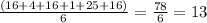
Finally, take the square root of the mean:

`\tt √(13)=3.605`

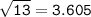
So, the standard deviation of Joey's data is approximately 3.605 minutes.

`\hrulefill`

For five-number summary:

The five-number summary is a way of summarizing a set of data by finding the minimum, first quartile (Q1), median, third quartile (Q3), and maximum.

In order to find the five-number summary for Joey's data, we first need to order the data from least to greatest:

50 50 52 55 58 59

• Minimum: The smallest value in the data set.
• First quartile (Q1): The middle number of the data below the median.
• Median: The middle number of the data set.
• Third quartile (Q3): The middle number of the data above the median.
• Maximum: The largest value in the data set.

By using definition:

Minimum: 50

First quartile (Q1): 50

Median:(52+ 55) / 2 =53.5

Third quartile (Q3):58

Maximum: 59