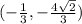Answer:
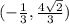 and
and
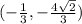
Explanation:
We know that the distance between some point
 and
and
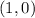 is
is
 where
where
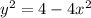 from the equation of the ellipse:
from the equation of the ellipse:
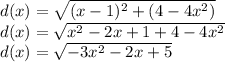
Distance is maximized where
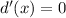 , and whatever that critical value is, we can get our x and y-coordinates of the points farthest from (1,0):
, and whatever that critical value is, we can get our x and y-coordinates of the points farthest from (1,0):
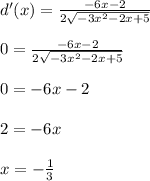
Now we can get the y-coordinate(s) of the point farthest from (1,0):
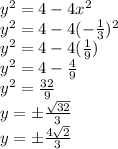
Therefore, the points on the ellipse that are the farthest from the point (1,0) are
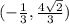 and
and