Answer:
10x + 5h - 3
Explanation:
evaluate f(x + h) by substituting x = x + h into f(x) , that is
f(x + h)
= 5(x + h)² - 3(x + h) + 4 ← expand factor using FOIL
= 5(x² + 2hx + h²) - 3(x + h) + 4 ← distribute parenthesis
= 5x² + 10hx + 5h² - 3x - 3h + 4
= 5x² + 10hx - 3x + 5h² - 3h + 4
now subtract f(x) from this expression
5x² + 10hx - 3x + 5h² - 3h + 4 - (5x² - 3x + 4) ← distribute parenthesis by - 1
= 5x² + 10hx - 3x + 5h² - 3h + 4 - 5x² + 3x - 4 ← collect like terms
= 10hx + 5h² - 3h ( factor out h from each term )
= h(10x + 5h - 3)
then
=
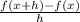
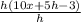← cancel h on numerator/ denominator
= 10x + 5h - 3