Question

1. [4] Evaluate the following definite integral. Be sure to show the substitution step if needed. a) \( \int_{4}^{25} \frac{2}{\sqrt{x}} d x \) b) \( \int_{2}^{3} 12\left(x^{2}-4\right)^{5} x d x \)

Answer 1

(a) 12

(b) 15,625

Explanation:

Part (a)

Given definite integral:

`\displaystyle \int_(4)^(25) (2)/(√(x)) \;dx`

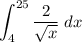
`\textsf{Apply the exponent rule:} \quad \frac{1}{\sqrt[n]{x}}=x^{-(1)/(n)}`

`\displaystyle \int_(4)^(25) (2)/(√(x)) \;dx=\int_(4)^(25) 2x^{-(1)/(2)} \;dx`

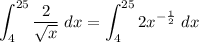
Evaluate the integral using the exponent rule:

`\begin{aligned} \displaystyle \int_(4)^(25) (2)/(√(x)) \;dx&=\displaystyle \int_(4)^(25) 2x^{-(1)/(2)} \;dx\\\\&=\left[\frac{2x^{-(1)/(2)+1}}{-(1)/(2)+1}\right]^(25)_(4)\\\\&=\left[\frac{2x^{(1)/(2)}}{(1)/(2)}\right]^(25)_(4)\\\\&=\left[4x^{(1)/(2)}\right]^(25)_(4)\\\\&=4(25)^{(1)/(2)}-4(4)^{(1)/(2)}\\\\&=4(5)-4(2)\\\\&=20-8\\\\&=12\end{aligned}`

`\hrulefill`

Part (b)

Given definite integral:

`\displaystyle \int_(2)^(3) 12\left(x^(2)-4\right)^(5) x \;dx`

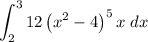
To evaluate the definite integral, use the method of substitution.

`\textsf{Let}\;\;u = x^2 - 4`

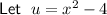
Find du/dx using the differentiation exponent rule, and rewrite it so that dx is on its own:

`(du)/(dx)=2x \implies dx=(1)/(2x)\;du`

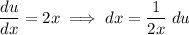
Find the new limits by substituting x = 2 and x = 3 into u = x² - 4:

`x = 2 \implies u=2^2-4=0`

`x=3 \implies u=3^2-4=5`

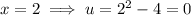
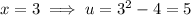
Rewrite the original integral in terms of u and du:

`\begin{aligned}\displaystyle \int_(2)^(3)12\left(x^(2)-4\right)^(5)x\;dx&=\int_(0)^(5)12\left(u\right)^(5)x\;(1)/(2x)\;du\\\\&=\int_(0)^(5)6u^(5)\;du\\\\\end{aligned}`

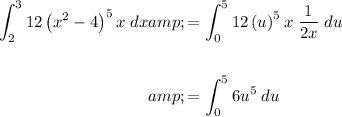
Evaluate the integral using the exponent rule:

`\begin{aligned}\displaystyle &=\left[(6u^(5+1))/(5+1)\right]^(5)_(0)\\\\&=\left[(6u^(6))/(6)\right]^(5)_(0)\\\\&=\left[\vphantom{\frac12}u^6\right]^(5)_(0)\\\\&=5^6-0^6\\\\&=15625-0\\\\&=15625\end{aligned}`

`\hrulefill`

Differentiation and integration rules used:

`\boxed{\begin{array}{c}\underline{\sf Differentiation\;Exponent\;Rule}\\\\\textsf{If}\;\; y=x^n,\;\textsf{then}\;\; \frac{\text{d}y}{\text{d}x}=nx^(n-1)\\\\\end{array}}`

`\boxed{\begin{array}{c}\underline{\sf Integration\;Exponent\;Rule}\\\\\displaystyle \int x^n\:\text{d}x=(x^(n+1))/(n+1)\;(+\;\text{C})\\\\\end{array}}`