Answer:
Approximately
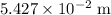 .
.
Step-by-step explanation:
For a planet of mass
 , the Schwarzschild Radius would be:
, the Schwarzschild Radius would be:
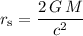 ,
,
Where:
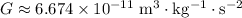 is the gravitational constant, and
is the gravitational constant, and
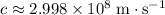 is the speed of light in vacuum.
is the speed of light in vacuum.
It is given that the mass of this planet is
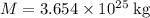 . Substitute this value into the expression for
. Substitute this value into the expression for
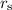 and evaluate to obtain:
and evaluate to obtain:
 .
.
In other words, if the radius of this planet goes below approximately
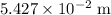 , the planet would become a black hole.
, the planet would become a black hole.