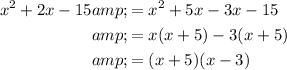Question

Factorise the follow

a) x² + 15x + 54
b) x² - 8x + 15
c) x²-2x-8
d) x² + 2x - 15

Answer 1

`\textsf{a)} \quad (x+6)(x+9)`

`\textsf{b)} \quad (x-3)(x-5)`

`\textsf{c)} \quad (x+2)(x-4)`

`\textsf{d)} \quad (x+5)(x-3)`

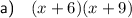
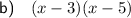
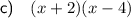
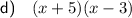
Explanation:

To factor the given quadratic expressions, we can use the method of factoring by grouping.

This technique involves splitting the middle term of a quadratic expression of the form ax² + bx + c into two terms such that the sum of their coefficients is equal to b, and the product of their coefficients is equal to ac.

`\hrulefill`

Part (a)

Given quadratic:

`x^2+15x+54`

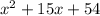
Therefore:

• a = 1
• b = 15
• c = 54

Two numbers that sum to 15 and multiply to 54 are 6 and 9. Therefore:

`\begin{aligned} x^2+15x+54&=x^2+6x+9x+54\\&=x(x+6)+9(x+6)\\&=(x+6)(x+9)\end{aligned}`

`\hrulefill`

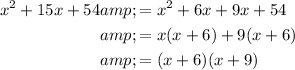
Part (b)

Given quadratic:

`x^2- 8x + 15`

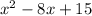
Therefore:

• a = 1
• b = -8
• c = 15

Two numbers that sum to -8 and multiply to 15 are -3 and -5. Therefore:

`\begin{aligned}x^2-8x+15&=x^2-3x-5x+15\\&=x(x-3)-5(x-3)\\&=(x-3)(x-5)\end{aligned}`

`\hrulefill`

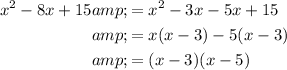
Part (c)

Given quadratic:

`x^2-2x-8`

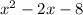
Therefore:

• a = 1
• b = -2
• c = -8

Two numbers that sum to -2 and multiply to -8 are 2 and -4. Therefore:

`\begin{aligned}x^2-2x-8&=x^2+2x-4x-8\\&=x(x+2)-4(x+2)\\&=(x+2)(x-4)\end{aligned}`

`\hrulefill`

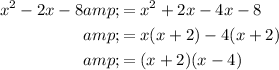
Part (d)

Given quadratic:

`x^2+ 2x - 15`

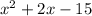
Therefore:

• a = 1
• b = 2
• c = -15

Two numbers that sum to 2 and multiply to -15 are 5 and -3. Therefore:

`\begin{aligned}x^2+2x-15&=x^2+5x-3x-15\\&=x(x+5)-3(x+5)\\&=(x+5)(x-3)\end{aligned}`