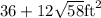Question

In 1485, Leonardo Da Vinci's sketched a parachute designs in the shape of square based pyramids. For a parachute design, he sketched it with square base having side lengths of 6 feet each and height of 7 feet. (i) How much air would be captured in the pyramid once it is deployed fully? (ii) How much canvas would require to make a parachute?​

Answer 1

i. 84 ft^3

ii. 36 + 12sqrt58 ft^2

Explanation:

To find out how much air would be captured in the parachute, we would need to find the volume of the pyramid.

The volume of a square pyramid is
`(a^2h)/(3)`, where a is the length of a side of the square base, and h is the height of the pyramid.

Since we know the square base has side length 6 and the height of the pyramid is 7, we can plug it in to find the volume = 84 ft^3.

To find how much canvas required to make the parachute, we need the surface area of the pyramid. Since a square pyramid consists of 4 congruent isosceles triangles and a square base, we can just find the area of the square base and one triangle for the total surface area.

Since the side length of the square is 6, the area of the square base is 36 ft^2.

Now to find the area of the isosceles triangles, we need to find the height and the base. Since we know the base length of the triangles is just the same as the side length of the square, it is 6 ft. To find the height of such a triangle, we realize that the height of the face triangle forms a right triangle with the height of the overall square pyramid and the square base. Since the height of the pyramid is 3 away from the edge, one leg is 3, and since the height of the pyramid is 7, the other leg of the triangle is 7.

Now, using Pythagorean theorem, we can find the height of one of the triangular faces:

`c^2=3^2+7^2\\c^2=58\\c=√(58)`

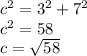
Now, we can find the area of one of the triangles (Note that the area of a triangle is 1/2 x base x height). Since the base is 6 and the height is the square root of 58, the area of one triangle is
`(6\cdot√(58))/(2)` =
`3√(58)`.

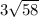Now the overall surface area is 4 times that plus 36 =
`36+12√(58)\text{ft}^2`