Question

A square piece of tin of side 18 cm is to be made into a box without a top, by cutting a square from each corner and folding up the flaps to form the box. What should be the side of the square to be cut off so that the volume of the box is the maximum possible?

Answer 1

The side of the square should be 3 cm

Explanation:

Let a square of side x be removed from each corner.

After removing the squares from the corner, the box will have dimensions:

length = 18 - 2x

breadth = 18 - 2x

height = x

The volumbe of a cuboid is :

V = lbh

= (18 - 2x)(18 - 2x)(x)

= (18 - 2x)²(x)

V = (18 - 2x)²(x)

differentiating w.r.t. x,

`(dV)/(dx) = (d)/(dx) [(18 - 2x)^2(x)]\\\\= x (d)/(dx) [(18 - 2x)^2] + (18 - 2x)^2(d)/(dx)(x)\\\\=x[2(18-2x)(-2)] + (18 - 2x)^2\\\\= -4x(18-2x) + (18 - 2x)^2\\\\= (18 - 2x)[-4x + 18-2x]\\\\=(18 - 2x)(18-6x)\\`

`(dV)/(dx) = 0\\ \\\Rightarrow (18-2x)(18-6x)=0\\\\\Rightarrow 18-2x=0 \;\;\;or \;\;\;18-6x=0\\\\\Rightarrow 2x=18 \;\;\;or \;\;\;6x=18\\\\\Rightarrow x=9 \;\;\;or \;\;\;x=3`

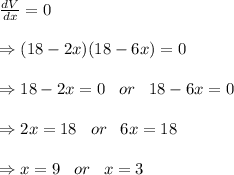
When x = 9,

length = 18 - 2x

= 18 - 2(9)

= 0

The length cannot be 0

∴ x = 9 is not possible

When x = 3,

length = 18 - 2x

= 18 - 2(3)

= 18 - 6

= 12

The length cannot be 0

∴ x = 9 is not possible

Check for maxima:

`(d^2V)/(dx^2) = (d)/(dx) ((dV)/(dx) )\\\\= (d)/(dx) [(18-2x)(18-6x)]\\\\= (18-6x)(d)/(dx) (18-2x)+(18-2x)(d)/(dx) (18-6x)\\\\= (18-6x)(-2)+(18-2x)(-6)`

When x = 3,

`(d^2V)/(dx^2) = (18-6x)(-2)+(18-2x)(-6)\\\\= -2[18 - 6(3)] -6 [18-2(3)]\\\\= -2(18 - 18) - 6(18-6)\\\\= - 6(12)\\\\= -72 < 0`

∴ x = 3 is a point of maxima.

The volume is maximised when x = 3