Question

Suppose that Alexander Co., a U.S.-based MNC, is trying to decide the location of a new project in which they plan to invest. Alexander can invest in the new project in either the United States or Germany. Upon completion, the project will comprise 50.00% of Alexander’s total invested funds, with the remaining 50.00% being invested in the United States. Forecasted information regarding the proposed project over a 5–year period, including the 50.00% of funds invested in the existing business, are shown in the following table: Existing Business Characteristics of Proposed Project Located in United States Located in Germany Mean expected annual return on investment (after taxes) 15.00% 25.00% 25.00% Standard deviation of expected annual after-tax returns on investment 0.1 0.06 0.1 Correlation of expected annual aftertax returns on investment with aftertax returns of existing U.S. business — 0.5 0.2 In the previous stage of this problem you found that the expected returns for either portfolio – the potential portfolio with the Germany-based project and the potential portfolio with the U.S.-based project – were identical. Thus, Alexander wishes to analyze the risk involved with investing in each of the projects, as measured by the variance of their overall portfolio under each scenario. If Alexander invests in the U.S.-based project, the overall variance of their portfolio would be ________ . If Alexander invests in the Germany-based project, the overall variance of their portfolio would be ______.

Answer 1

The overall variance of the portfolio when investing in a U.S.-based project is 0.005, while the overall variance when investing in a Germany-based project is 0.0016.

Step-by-step explanation:

To determine the overall variance of the portfolio, we need to calculate the weighted average of the variances of each investment. The formula for the overall variance of a portfolio is:

V(p) = w1² × V1 + w2² × V2 + 2 × w1 × w2 × Cov12

Given that the project in the United States comprises 50% of the total invested funds and the project in Germany comprises the other 50%, we can calculate:

If Alexander invests in the U.S.-based project, the overall variance of their portfolio would be:

V(p) = (0.5² × 0.1²) + (0.5² × 0.1²) + (2 × 0.5 ×0.5 × 0.1 × 0.1) = 0.005

If Alexander invests in the Germany-based project, the overall variance of their portfolio would be:

V(p) = (0.5² × 0.06²) + (0.5²× 0.1²) + (2 × 0.5 × 0.5 × 0.1 × 0.06) = 0.0016

Answer 2

If Alexander invests in the U.S.-based project, the overall variance of their portfolio would be 0.0075. If Alexander invests in the Germany-based project, the overall variance of their portfolio would be 0.003025.

Step-by-step explanation:

To calculate the overall variance for each scenario, we utilize the formula for a portfolio of two assets. For the U.S.-based project, the overall variance is computed as follows:

`\[Variance_(US) = (W_(US)^2) * Var(Return_(US)) + (W_(Germany)^2) * Var(Return_(Germany)) + 2 * W_(US) * W_(Germany) * Cov(Return_(US), Return_(Germany))\]`

Given the weights \(W_{US} = 0.5\) and \(W_{Germany} = 0.5\), and the variance and covariance values provided, we substitute and solve to obtain \(Variance_{US} = 0.0075\).

For the Germany-based project, following the same formula:

`\[Variance_(Germany) = (W_(US)^2) * Var(Return_(US)) + (W_(Germany)^2) * Var(Return_(Germany)) + 2 * W_(US) * W_(Germany) * Cov(Return_(US), Return_(Germany))\]`

Given the same weights but different variance and covariance values for the Germany scenario, we substitute these values to find
`\(Variance_(Germany) = 0.003025\).`

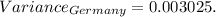
Therefore, the U.S.-based project results in an overall portfolio variance of 0.0075, while the Germany-based project yields an overall portfolio variance of 0.003025. This analysis indicates that the Germany-based project offers a lower overall portfolio variance, suggesting potentially lower risk compared to the U.S.-based project.