Question

Do the question please ​

Answer 1

Because our p-value is less than α (0.001<0.05), we reject the null hypothesis. There is evidence to conclude that there is a difference in the distributions of wine purchases at this store when no music, French accordion music, or Italian string music is played. However, because the independence condition was not met, these results may not be accurate.

Explanation (courtesy of my stats notes):

We will run a chi-square test for homogeneity in order to determine if the distributions of the wine purchases under different music treatments are similar or different.

We want to test at
`\alpha = 0.05`:

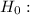`H_0:` There is no difference in the distributions of wine purchases at this store when no music, French accordion music, or Italian string music is played.

`H_a` : There is a difference in the distributions of wine purchases at this store when no music, French accordion music, or Italian string music is played.

Next, we must check the conditions.

Random: There were three randomly assigned treatments (the three types of music); the random condition is satisfied.

Large Sample Size: See table of expected counts - all expected counts
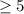`\ge 5`; the large sample size condition is satisfied.

Independent: The independent condition is not met because customers may buy several bottles of the same type of wine, so proceed with the test with caution.

Table of expected counts (row total*column total/total):

`\left[\begin{array}{ccc}34.22&30.56&34.22\\10.72&9.57&10.72\\39.06&34.88&39.06\end{array}\right]`

The chi-square statistic is then:
`\chi ^2 = \Sigma ((O-E)^2)/(E)=((30-34.22)^2)/(34.22)+\cdots+((35-39.06)^2)/(39.06)=18.28`.

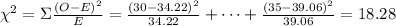The chi-square statistic has
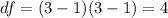`df = (3-1)(3-1) = 4` ((rows-1)(columns-1)).

The p-value is then
`P(\chi ^2 > 18.28) \approx 0.001`.