Question

Q 8 (10 points) Double integrals over nonrectangular regions. Describe the region of integration and sketch it for the following setup. Then reverse the order of integration and evaluate. ∫04​∫​y2​9x3+1​dxdy

Answer 1

52

Explanation:

The given region of integration is
`D=\(x,y)`

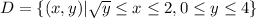
By reversing the order of integration, the region is now
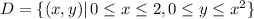`D=\(x,y)`, making the integral easier to evaluate:

`\displaystyle \int^4_0\int^2_(√(y))9√(x^3+1)\,dx\,dy\\\\=\int^2_0\int^(x^2)_09√(x^3+1)\,dy\,dx\\\\=\int^2_09x^2√(x^3+1)\,dx`

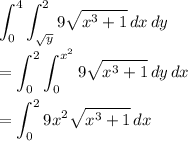
Let
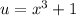`u=x^3+1` and
`du=3x^2\,dx` so that
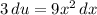`3\,du=9x^2\,dx`. Bounds become
`u=0^3+1=1` to
`u=2^3+1=9`

`\displaystyle 3\int^9_1√(u)\,du\\\\=3\biggr((2)/(3)u^(3)/(2)\biggr)\biggr|^9_1\\\\=3\biggr((2)/(3)(9)^(3)/(2)\biggr)-3\biggr((2)/(3)(1)^(3)/(2)\biggr)\\\\=2(27)-2(1)\\\\=54-2\\\\=52`

I've attached a graph to this answer for a visual, so I hope it helps!