Question

A bullet is shot upwards with an initial velocity of 200ft/sec from a point 10ft above the ground, and its height above the ground at time t is given by h(t)=−25t

2
+200t+10 i. How high will the bullet go? ft ii. How long will it take the bullet to reach the highest point? sec

Answer 1

The bullet will reach a height of 410 feet and it will take 4 seconds to reach the highest point.

Step-by-step explanation:

To determine the height the bullet will go, we need to find the maximum point of the trajectory.

The maximum point occurs when the bullet reaches its highest height.

To find this, we can find the vertex of the quadratic equation representing the bullet's height.

The formula for the height at time t is h(t) = -25t^2 + 200t + 10.

The vertex of this equation is given by the formula t = -b/2a, where a = -25 and b = 200.

Substituting these values, we get t = -200/(2*(-25)) = -200/-50 = 4 seconds.

So, the bullet will reach its highest point in 4 seconds.

To find the maximum height, we substitute the value of t = 4 into the equation h(t).

`h(4) = -25(4)^2 + 200(4) + 10`

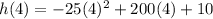
= -25(16) + 800 + 10

= -400 + 800 + 10

= 410 feet.

Therefore, the bullet will reach a height of 410 feet.