Question

2. As part of a study of natural variation in blood chemistry, serum potassium concentrations were measured in 66 randomly selected healthy women. The sample mean concentration was 4.36mEq/1, and the sample standard deviation was 0.42mEq/l. (a) Find the lower bound for the 95% confidence interval for the true serum potassium concentrate in healthy women. (b) Find the upper bound for the 95% confidence interval for the true serum potassium concentrate in healthy women. (c) Interpret your confidence interval found in (a,b) in terms of the problem. (d) Does your interval support the claim that normal serum potassium concentrations are above 2.3 ? (e) If we were to build a 99% confidence interval instead, would it widen or narrow? 3. Continue with the data from Problem 1 (The women menstrual cycle length). (a) If we wanted our confidence interval to have a margin of error of 0.5 days at 90% confidence, how many women should we sample (at least)? (b) If we wanted our confidence interval to have a margin of error of 0.1 days at 90% confidence, how many women should we sample (at least)? (c) What tends to happen to the sample size we need as the margin of error decreases? You may assume everything else remains constant. (d) What tends to happen to the sample size we need as the standard deviation increases? You may assume everything else remains constant.

Answer 1

(a) The lower bound for the 95% confidence interval is approximately

`\(4.36 - (1.96 * (0.42)/(√(66)))\) mEq/L.`

(b) The upper bound for the 95% confidence interval is approximately

`\(4.36 + (1.96 * (0.42)/(√(66)))\) mEq/L.`

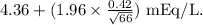
(c) The 95% confidence interval for the true serum potassium concentration in healthy women is between the lower and upper bounds calculated in (a) and (b). This interval provides a range of values within which we are 95% confident that the true serum potassium concentration lies.

(d) If the interval includes 2.3, then we do not have enough evidence to support the claim that normal serum potassium concentrations are above 2.3.

(e) A 99% confidence interval would widen because the critical value (1.96) used in the margin of error calculation for a 95% confidence interval is smaller than the critical value (2.576) for a 99% confidence interval. A higher confidence level requires a wider interval.

Step-by-step explanation:

(a) To find the lower bound, we use the formula
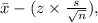`\( \bar{x} - (z * (s)/(√(n))) \),` where
`\( \bar{x} \)` is the sample mean, ( z ) is the Z-score corresponding to the desired confidence level (1.96 for 95%), ( s ) is the sample standard deviation, and ( n ) is the sample size.

(b) To find the upper bound, we use the formula

`\( \bar{x} + (z * (s)/(√(n))) \).`

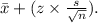
(c) The interpretation of the confidence interval is that we are 95% confident that the true serum potassium concentration in healthy women falls between the calculated lower and upper bounds.

(d) If the interval contains 2.3, we cannot reject the claim that normal serum potassium concentrations are above 2.3.

(e) The wider interval for a 99% confidence level is due to the higher Z-score (2.576), indicating a greater range to capture a higher percentage of the distribution.