Question

The length of a square equals (x+5) units. The width of the square equals (5x-11) units. What is the area of the square?

Answer 1

Explanation:

To find the area of the square, we need to multiply the length by the width. In this case, the length is represented by (x + 5) units and the width is represented by (5x - 11) units.

Area of the square = length * width

Area = (x + 5) * (5x - 11)

Expanding the expression:

Area = 5x^2 + 25x - 11x - 55

Combining like terms:

Area = 5x^2 + 14x - 55

Therefore, the area of the square is given by the expression 5x^2 + 14x - 55.

Answer 2

Hi there!

The question is asking us to find the rectangle's area.

To find the area, we use the formula:

`\pmb{A=l* w}`

Here,

◈ A = area

◈ l = length

◈ w = width

In this problem,

◈ A is unknown

◈ l = (x + 5) units

◈ w = (5x - 11) units

◈◈◈◈◈◈◈◈◈◈◈◈◈◈◈◈◈◈◈

Plug in the data :-

`\pmb{A=(x+5)(5x-11)}`

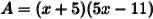
To simplify, use FOIL :-

◈ First

◈ Outside

◈ Inside

◈ Last

Multiply the first terms : 5x * x = 5x²

Multiply the outside terms : x * (-11) = -11x

Multiply the inside terms : 5 * 5x = 25x

Multiply the last terms: 5 * (-11) = -55

Combine the terms: 5x² - 11x + 25x - 55

5x² + 14x - 55

Therefore, the rectangle's area is 5x² + 14x - 55 square units.

Have a fantastic day!

◈◈◈◈◈◈◈◈◈◈◈◈◈◈◈◈◈◈◈