Question

A certain spring found not to obey Hooke's law exerts a restoring force $Fx(x) = -ax - \beta x^2$ if it is stretched or compressed, where $\alpha$ = 60.0 N/m and $\beta$ = 18.0 N/m2. The mass of the spring is negligible. (a) Calculate the potential-energy function U($x$) for this spring. Let $U = 0$ when $x = 0$. (b) An object with mass 0.900 kg on a frictionless, horizontal surface is attached to this spring, pulled a distance 1.00 m to the right (the $+x$-direction) to stretch the spring, and released. What is the speed of the object when it is 0.50 m to the right of the $x = 0$ equilibrium position?

Answer 1

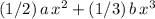`(1/2)\, a\, x^(2) + (1/3)\, b\, x^(3)`, which is equivalent to
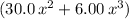`(30.0\, x^(2) + 6.00\, x^(3))` joules when
`x` is in meters.

Approximately
`7.85\; {\rm m\cdot s^(-1)}`.

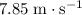Step-by-step explanation:

(a)

Integrate the restoring force to obtain the potential-energy equation:

`\begin{aligned}U(x) &= U(0) + \int\limits^(x)_(0) -F(s)\, ds \\ &= U(0) + \int\limits^(x)_(0) \left( a\, s + b\, s^(2)\right)\, ds \\ &= 0 + \left[(1)/(2)\, a\, s^(2) + (1)/(3)\, b\, s^(3)\right]_(0)^(x) \\ &= (1)/(2)\, a\, x^(2) + (1)/(3)\, b\, x^(3)\end{aligned}`.

When
`x` is measured in joules, the value of
`U(x)` measured in joules would be:

`\begin{aligned}U(x) &= (1)/(2)\, a\, x^(2) + (1)/(3)\, b\, x^(3) = 30.0\, x^(2) + 6.00\, x^(3)\end{aligned}`.

(b)

As the object travels from
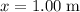`x = 1.00\; {\rm m}` to
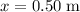`x = 0.50\; {\rm m}`, the difference in the potential energy in the spring would be converted into kinetic energy:

`\begin{aligned} \text{KE} &= \left[U(1.00) - U(0.50)\right]\; {\rm J} \\ &= \left[36 - 8.25\right]\; {\rm J} \\ &= 27.75\; {\rm J}\end{aligned}`.

Since
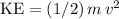`\text{KE} = (1/2)\, m\, v^(2)`, rearrange and solve for
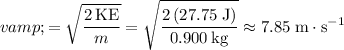`v`:

`\begin{aligned}v &= \sqrt{\frac{2\, \text{KE}}{m}} = \sqrt{\frac{2\, (27.75\; {\rm J})}{0.900\: {\rm kg}}} \approx 7.85\; {\rm m\cdot s^(-1)}\end{aligned}`.