Question

100 Points

Check Pictures (Only 3 Questions)
(Must Show Work)
If I Fail this, I Might Fail the Grade!!!

Answer 1

2nd Question:

`\boxed{\tt \tt z^7 = 10^7 *cos((7\pi)/(3)) +10^7* i*sin((7\pi)/(3))}`

3rd Question:

• 28.2 miles West and 10.3 miles South

Explanation:

1st question: Attachment

2nd question:

De Moivre's Theorem is a theorem in complex analysis that states that the nth power of a complex number z = r(cos θ + i sin θ) is given by:

zn = r^n * (cos nθ + i sin nθ)

where r is the modulus of z and θ is the argument of z.

For the question:

To evaluate the expression (5 + 5√3i)^7` using de Moivre's theorem, we can express the number in polar form and then apply the theorem.

Let's start by converting the number to polar form.

Given: z = 5 + 5\sqrt{3}

comparing with z = a+bi

we get, a=5 and b=
`5√(3)`

In order to convert z to polar form, we need to find its magnitude(r) and argument (θ).

Magnitude (r):

The magnitude of 'z' is calculated as follows:

`\tt |r| = √(a^2 + b^2)\\|r| = \sqrt{(5^2 + (5√(3))^2}\\|r| =10`

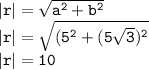
Argument (`θ`):

The argument of `z` is calculated as follows:

`\tt \theta = Tan^(-1)((b)/(a))\\\theta = Tan^(-1)((5√(3))/(5))\\\theta =(\pi)/(3)`

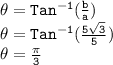
Now that we have r = 10 and θ = π/3, we can express z in polar form:

`\tt z = 10(cos((\pi)/(3)) + i*sin((\pi)/(3)))`

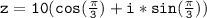
Now let's apply de Moivre's theorem, which states that for any complex number z = r(cosθ + i*sinθ) and any positive integer n, and the nth power of z can be calculated as follows:

`\tt z^n = r^n * (cos(n\theta) + i*sin(n\theta))`

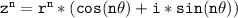
In our case, n = 7:
`\theta=(\pi)/(3)`

`\tt z^7 = 10^7 * (cos((7\pi)/(3)) + i*sin((7\pi)/(3)))`

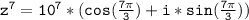
The final answer, in rectangular form, is:

`\boxed{\tt \tt z^7 = 10^7 *cos((7\pi)/(3)) +10^7* i*sin((7\pi)/(3))}`

`\hrulefill`

Question no. 3

Given:

• Speed of helicopter = 90 mph
• Bearing = 250°
• Time = 20 minutes = 20/60 hours = 1/3 hours

Solution:

Distance traveled = speed * time

= 90 * (1/3)

= 30 miles

Horizontal component = distance * cos(bearing)

= 30 * cos(250°)

= -10.3 miles

Vertical component = distance * sin(bearing)

= 30 * sin(250°)

= -28.2 miles

Location of helipad = (-10.3, -28.2) miles, which is about 28.2 miles West and 10.3 miles South of the airport.