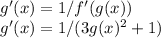Question

Find the derivate of the inverse for f(x)=x^3+x-2

Answer 1

If we let the inverse be g(x) then,

The derivative is,

`g'(x) = 1/(3g(x)^2+1)`

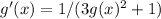
(Don't see a further way of simplifying)

Explanation:

First, we find the derivative of f(x),

`f(x) = x^3+x-2\\taking \ the \ derivative,\\f'(x) = 3x^2 + 1\\`

We can also write this as,

`dy/dx = 3x^2 + 1`

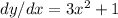
Now, to find the derivative for the inverse, we find dx/dy, so,

`dy = (3x^2+1)dx\\dx/dy = 1/(3x^2+1)\\`

Now, writing it in terms of the inverse, the best we can do is,

let
`g(x) = f^(-1)(x)`

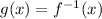
then,

`g'(x) = 1/f'(g(x))\\g'(x) = 1/(3g(x)^2+1)`