Answer:
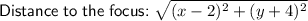
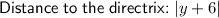
Explanation:
Distance to the focus
The focus of a parabola is a fixed point located on the axis of symmetry, such that all points on the parabola are equidistant to both the focus and the directrix. It is located inside the parabola. Therefore, the focus of the given parabola is (2, -4).
To find the distance from a point (x, y) to the focus of the parabola, we can use the distance formula:

Let the focus be the first point: (x₁, y₁) = (2, -4)
Let (x, y) be the second point: (x₂, y₂) = (x, y)
Substitute the points into the distance formula:

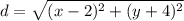
Therefore, the distance to the focus is:
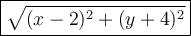

Distance to the directrix
The directrix of a parabola is a fixed line outside of the parabola that is perpendicular to the axis of symmetry. Therefore, the directrix of the given parabola is y = -6.
The distance from any point on the parabola to the directrix is the absolute value of the difference between the y-coordinate of the point and the y-coordinate of the directrix. Therefore:

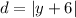
Therefore, the distance to the directrix is:
